Chapter 2 メタ分析

メタ分析 (meta-analysis) とは、複数の研究の結果を統合 (pool) し分析すること、またはそのための手法や統計解析のことです。 システマティックレビューで文献をくまなく探し、その結果をメタ分析することが典型的な方法です。

メタ分析については、R には多くのパッケージがあり、公式サイト中にも Michael Dewey によるメタ分析のパッケージの紹介ページがあります。

https://cran.r-project.org/web/views/MetaAnalysis.html

また、Minds 診療ガイドライン作成マニュアル2020 ver. 3.0 には、複数の事例とサンプルコードが解説されています。

R以外のソフトウェアとしては、メタ分析を推奨している Cochrane から RevMan をいうソフトウェアを無償で提供しています。

2.1 メタ分析の手法

メタ分析は、参照する文献が用いている統計手法によって違いが出てきます。

  1. システマティックレビューによって抽出された論文からデータを取得する
  • データがない場合は、コレスポンディングオーサーにデータを請求する
  • 生データ（個人データ, Individual Participant Data）を取得する場合もある
  1. 固定効果、ランダム効果を選択する、あるいは weight を計算する
  2. データを統合 (pool) する
  3. 異質性 (heterogeneity) を検証する
  4. 出版バイアスを検証する

2.2 論文 Abate SM (2020) PLoS One

実際の論文をもとに、比率 (proportion) のメタ分析を行ってみましょう。 ここで、比率 (proportion) とは、ある母集団に対して特定の特徴を持った人の比率です。

なお、rate と proportion の用語は、ここでは深入りしません。

Abate SM, Ahmed Ali S, Mantfardo B, & Basu B (2020). Rate of Intensive Care Unit admission and outcomes among patients with coronavirus: A systematic review and Meta-analysis. PloS one, 15(7), e0235653. https://doi.org/10.1371/journal.pone.0235653

コロナウィルス感染患者の ICU admission のデータです。いわゆる新型コロナ (SARS-COV-2) だけではなく、SARS や MERS のコロナウィルスも含めて、ICU入室率を扱う論文を集めてメタ分析しています。

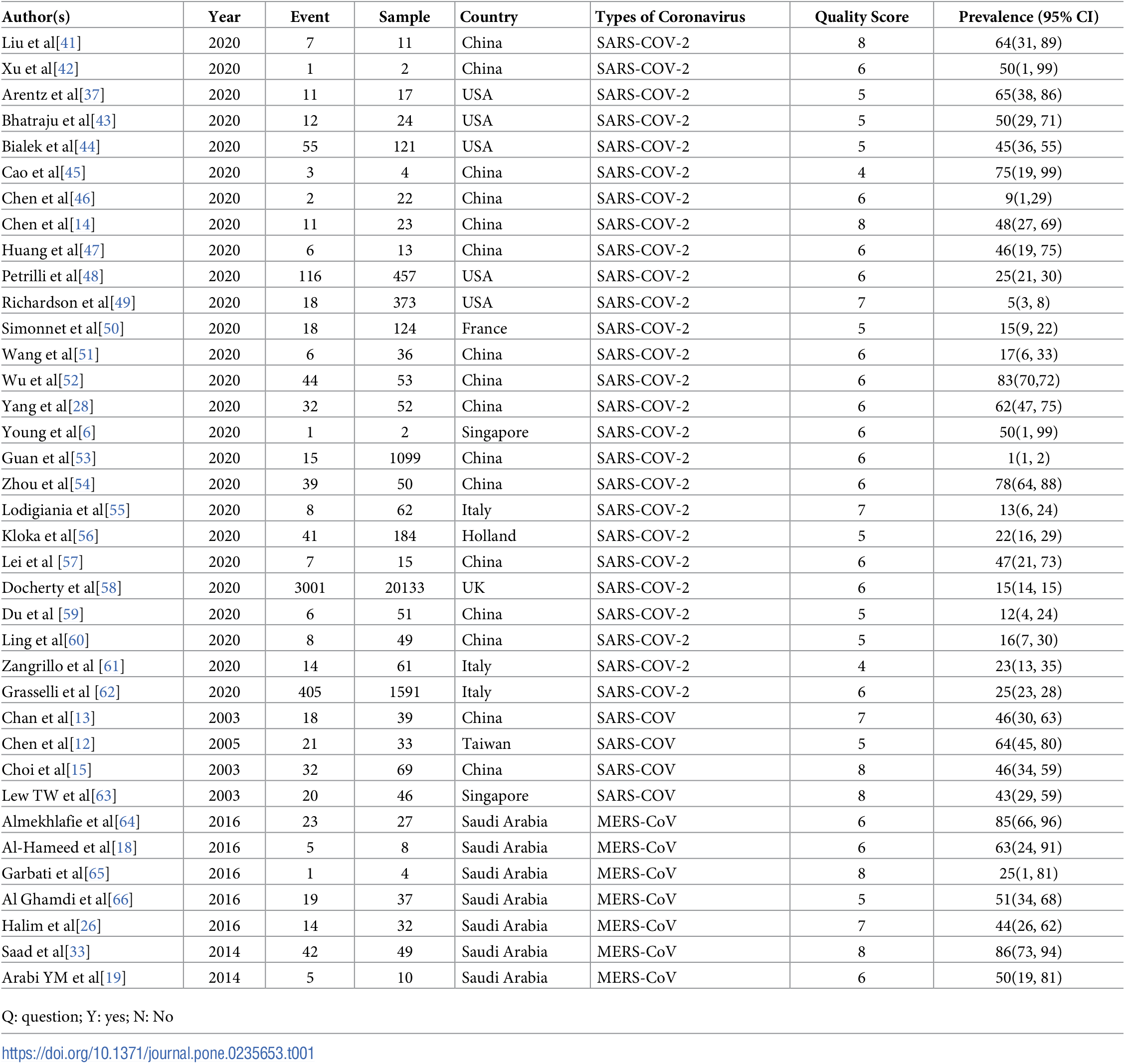
Abate (2020) Table 1. Methodological quality of included studies.

Figure 2.1: Abate (2020) Table 1. Methodological quality of included studies.

論文中に示されている全体のフォレストプロットです。

フォレストプロットは、以下のように読み取ります。

  • 各行は一つの研究論文を示しています。
  • 数値は、ICU入室率 [その95%信頼区間] を示しています。
  • 点はICU入室率を示し、点の大きさはサンプルサイズを示しています。
  • 点を中心とした線は95%信頼区間を示しています。
  • 一番最後の行は統合 (pool) されたものです。四角の代わりに菱形を使います。
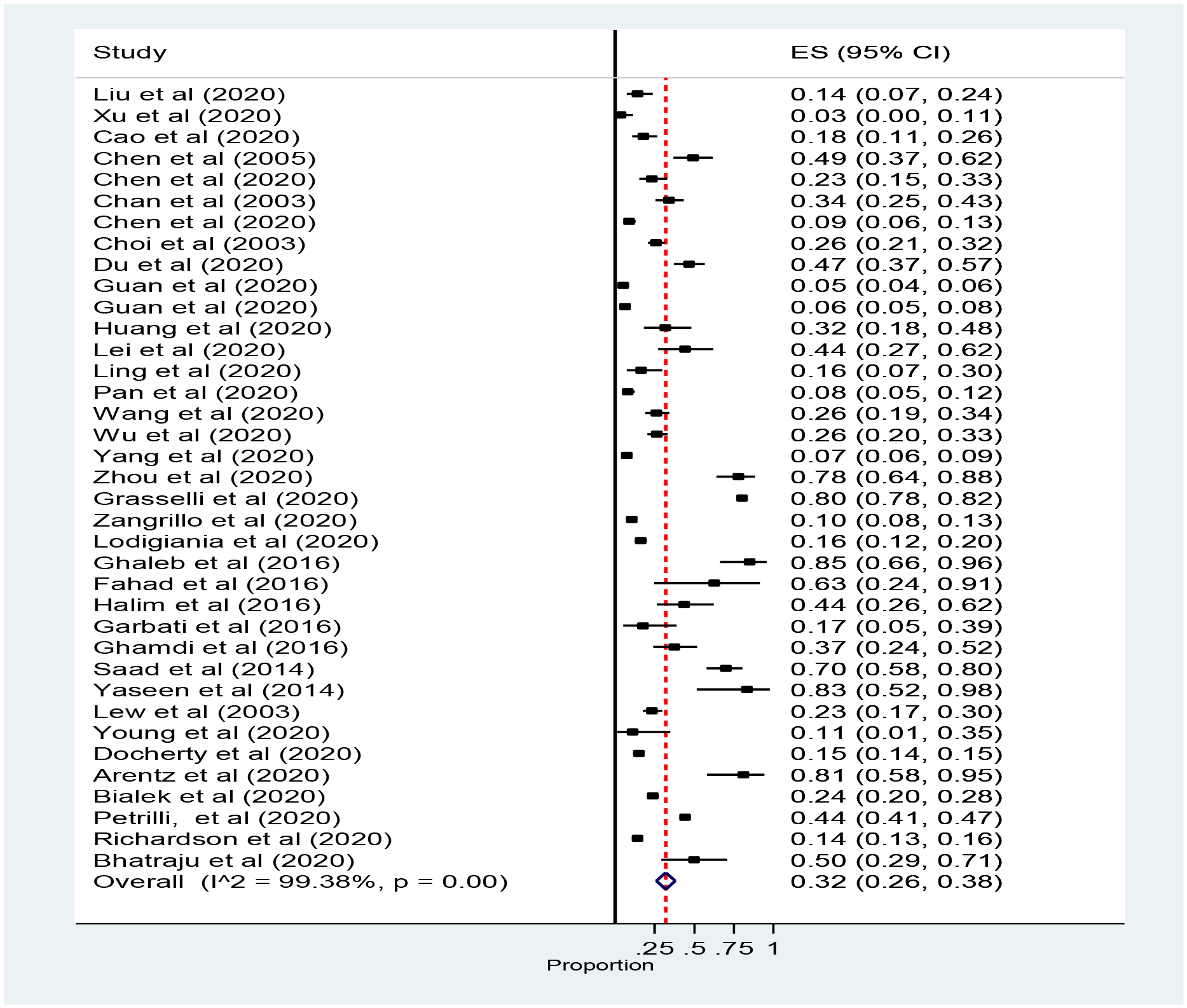
Abate (2020) Fig 2. Forest plot for the prevalence of ICU admission patients with coronavirus.

Figure 2.2: Abate (2020) Fig 2. Forest plot for the prevalence of ICU admission patients with coronavirus.

2.3 パッケージと関数

メタ分析を一度に行ってくれるのが meta パッケージです。 メタ分析は、対象となる統計手法に応じて統合 (pool) 方法も変わります。 meta は、以下のような関数を提供しています。

  • metacont: ２群の連続変数
  • metabin: ２群の２値変数
  • metainc: ２群の発症 (incidence) 率
  • metacor: 相関係数 (１群)
  • metamean: 平均値 (１群)
  • metaprop: proportion (１群) 引数 event(イベント数) と n(観察数)
  • metarate: 発症 (incidence) 率 (１群) 引数 event(イベント数)と person time

2.4 CSVデータの読み込み

library(readr)
dfMeta <- read_csv("https://ndownloader.figshare.com/files/23167073")
## Rows: 38 Columns: 7
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr (4): Author, country, corona, Study design
## dbl (3): year, event, sample
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

列ごとにデータ型が示されていることが分かります。

  • Author: 文字列
  • year: 数値（小数点）
  • event: 数値（小数点）
  • sample: 数値（小数点）
  • country: 文字列
  • corona: 文字列
  • Study design: 文字列

ここで、Study design は、列名に空白があるので、バッククォート記号で囲みます。

データ型は、csv 以外では示されないようです。なぜでしょうか？

列名は概ね一貫していますが、Author と Study design のみ大文字から始まり、他は小文字から始まっています。 また、Study design は空白が入っています。 大文字小文字は大きな影響はありませんが、空白は厄介です。 このため、Study design は、バッククォート記号で囲みます。

バッククォート記号は、日本語キーボードの場合、SHIFT キーを押しながら @ を押します。

dfMeta <- na.omit(dfMeta)
dfMeta$Study_design <- dfMeta$`Study design`

関数

  • na.omit: NA のある行を削除する。

元データの最後の行は空データで、おそらく元々は統合データを格納するために準備してあったと思われます。 この行は不要なので、NA データのある行を削除しました。

R では、データの入っていないことを表す手段が複数あります。NULL や NA です。NA などがあるとエラーが出やすくなります。

2.5 meta でメタ分析

meta ライブラリの metaprop 関数を使います。

library(meta)
mpResult <- metaprop(data = dfMeta, 
                event = event, 
                n = sample, 
                studlab = paste(Author, year))

関数

  • paste: 文字列をつなげる。文字列間 (sep) にはデフォルトで空白が追加される。 ここでは、Author と year を空白でつなげている。

変数と引数

  • mpResult は、metaprop の結果を格納します。MetaProp から mp をとって mpResult と命名しました。
  • 引数 data は、データフレーム dfMeta としました。
  • 引数 event は、データフレーム中の event (イベント数) 列を指定しました。
  • 引数 n は、データフレーム中の sample (観測数) 列を指定しました。
  • 引数 studlab は、データフレーム中の Author (著者) 列と year (発行年) をつなげたものを指定しました。

結果を見てみます。

mpResult
## Number of studies combined: k = 37
## Number of observations: o = 32741
## Number of events: e = 6220
## 
##                      proportion           95%-CI
## Common effect model      0.1900 [0.1858; 0.1943]
## Random effects model     0.2834 [0.2057; 0.3765]
## 
## Quantifying heterogeneity:
##  tau^2 = 1.6165; tau = 1.2714; I^2 = 99.0% [98.8%; 99.1%]; H = 9.83 [9.26; 10.44]
## 
## Test of heterogeneity:
##        Q d.f. p-value             Test
##  3481.43   36       0        Wald-type
##  4446.74   36       0 Likelihood-Ratio
## 
## Details on meta-analytical method:
## - Random intercept logistic regression model
## - Maximum-likelihood estimator for tau^2
## - Logit transformation

結果においては、異質性 (heterogeneity) 検定の結果が示されています。 Q, \(\tau^2\), \(I^2\) などが異質性の指標です。

\(I^2\)

  • 0 〜40%（重要でない異質性）
  • 30 〜60%（中等度の異質性）
  • 50 〜90％（大きな異質性）
  • 75 〜100%（高度の異質性）
forest(mpResult)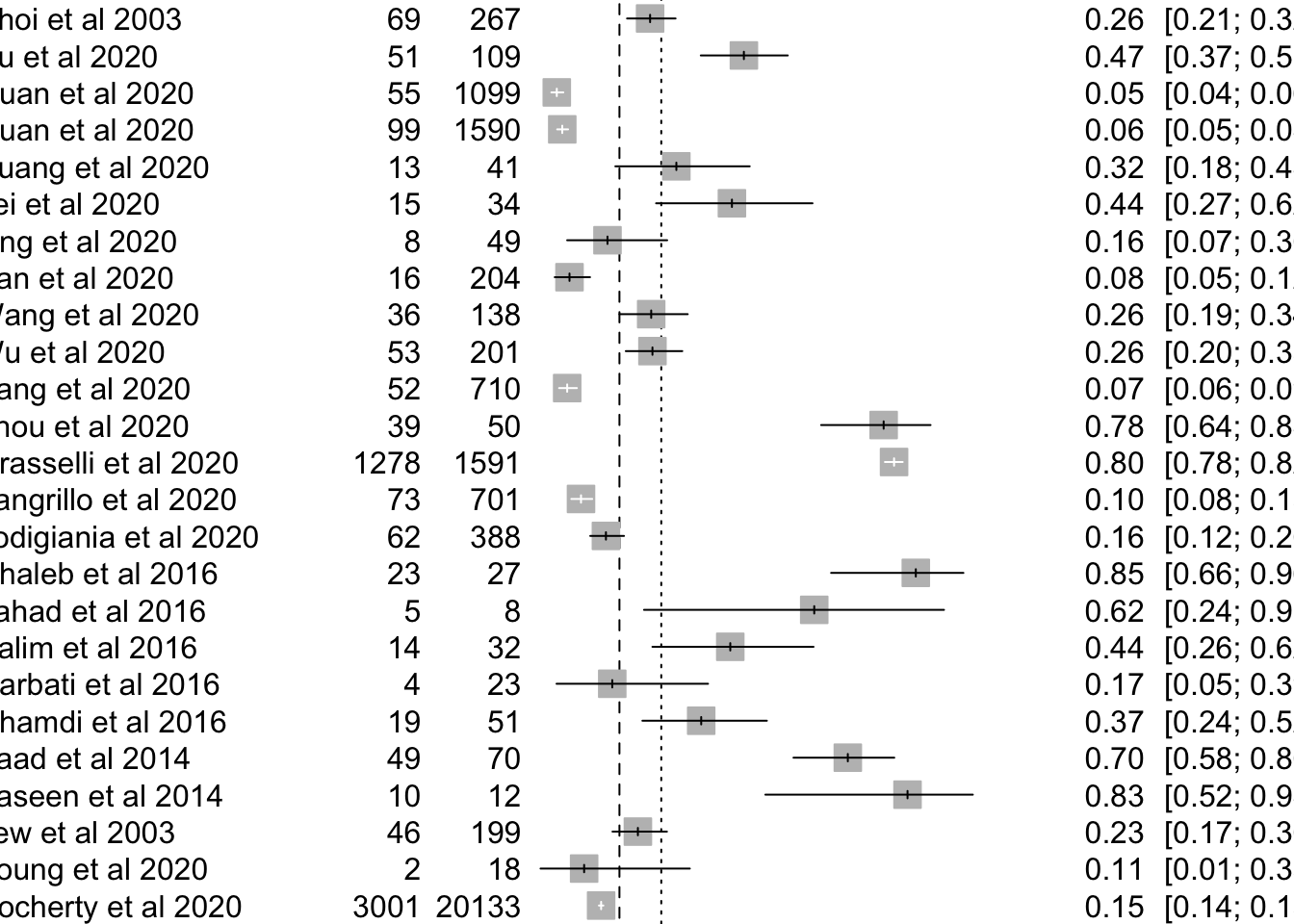

あまり美しくないので、オプションを試してみます。

forest(mpResult, 
       layout = "RevMan5", 
       comb.fixed = FALSE,
       label.right = "Favours control", 
       col.label.right = "red",
       label.left = "Favours experimental", 
       col.label.left = "green",
       prediction = TRUE)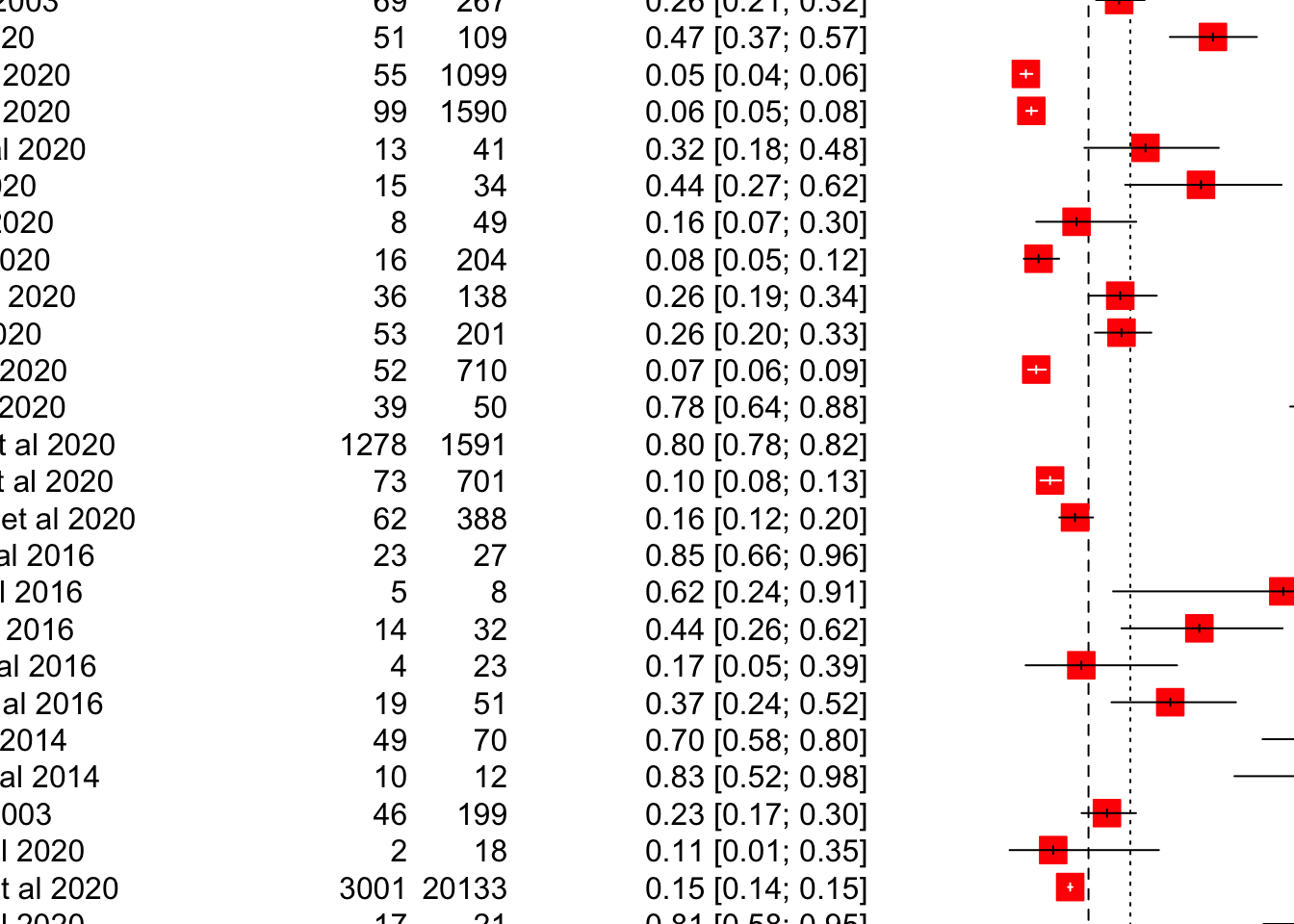

2.6 出版バイアス

これまで、研究はポジティブな結果が出た時に発表される傾向がありました。これはメタ分析を行う際にはバイアスとなってしまいます。これを出版バイアスと言います。多くの論文では、ファンネルプロットを作成して、視覚的に出版バイアスがあるかどうかを確認するに止まります。

2.6.1 ファンネルプロット

ファンネルプロットを描いてみます。

funnel(mpResult)

2.6.2 Egger 検定

メタ分析の論文では、出版バイアスがあるかどうかをファンネルプロットで視覚的に確認したというものが多く見られます。 しかしながら、出版バイアスを検証する統計もあります。

metabias(mpResult)
## Linear regression test of funnel plot asymmetry
## 
## Test result: t = 1.40, df = 35, p-value = 0.1698
## 
## Sample estimates:
##    bias se.bias intercept se.intercept
##  2.8392  2.0256   -1.5860       0.1907
## 
## Details:
## - multiplicative residual heterogeneity variance (tau^2 = 94.1829)
## - predictor: standard error
## - weight:    inverse variance
## - reference: Egger et al. (1997), BMJ

このデータに対し、Egger 検定を行ったところ、

  • p = 0.1698

となり、出版バイアスはあるとは言えません。