Chapter 3 スクリーニングツールの開発
3.1 ゴールドスタンダードとスクリーニング
3.1.1 ゴールドスタンダード
criterion standard (also known as reference standard): test considered to be the diagnostic standard for a particular diseas or condition, used as a basis of conparison for other (usually noninvasive) tests. An outdated term is gold standard, which refers to a time when the monetary system was based on the value of gold. This is no longer the case and the term is obsolete.
現在では、ゴールドスタンダードという言葉は推奨されておらず、標準基準 (criterion standard)や参照基準(reference standard)と言います。
AMA Manual of Style 11th ed p. 1031
3.1.2 スクリーニング
スクリーニングの Wilson 基準(最新版)
- 検査プログラムは、認識されている必要性に対応しなければならない
- まず最初に、検査の目的が定められていること
- 対象となる母集団の定義が定められていること
- 検査プログラムの有効性に科学的な証拠があること
- 計画は、周知活動、検査・医療補助・プログラム管理に統一性がなければならない
- 検査のもつ潜在的なリスクを最小限にするメカニズムを有した高度な品質が保証されていること
- 計画は、情報に関する権利と守秘性を確保し、自主性を尊重しなければならない
- 計画は、対象集団の全員が公平にスクリーニングを受ける機会を得られるよう促進すべきである
- プログラムに対する評価は、事前に計画されていなければならない
- スクリーニングによって与えられる損失より、得られる利益のほうが勝っていなければならない
3.2 感度と特異度
疫学では、様々な指標が用いられています。 医学や心理学では、さまざまな検査が用いられていますが、その中でも感度 (sensitivity) と特異度 (specificity) は評価やスクリーニングの妥当性を検証する際に用いられる尺度です。 感度と特異度は、それほど難しい計算ではありません。
| Disease + | Disease - | |
|---|---|---|
| Test + | A | B |
| Test - | C | D |
感度 = \(\dfrac{A}{A + C}\)
特異度 = \(\dfrac{D}{B + D}\)
3.3 有病率と感度・特異度
ある検査の感度が60%、特異度が99%とします。 1万人のうち0.1%にあたる10人が感染しているとします。
| Disease + | Disease - | |
|---|---|---|
| Test + | 6 | 100 |
| Test - | 4 | 9890 |
感度 = \(\dfrac{6}{6 + 4} = 60.0%\)
6/(6+4)## [1] 0.6特異度 = \(\dfrac{9890}{100 + 9890} = 99.0%\)
9890/(100+9890)## [1] 0.98999これを解釈すると以下のようになります。 1万人にこの検査を行ったところ、106人の陽性者が出ました。 このうち、真陽性者は6人、そして陽性的中率は、わずかに \(\dfrac{6}{6 + 100} = 5.7\%\) となります。 つまり、感度と特異度の解釈は、有病率に大きく影響を受けることがわかります。
3.4 ROC曲線
- x軸を 偽陽性率 (1-特異度)、y軸を感度とする。
- 検査値ごとの感度、特異度をプロットする。
- 点をつなぐ(これを、Receiver Operator Curve, ROC という)
- 全体の面積を1としたときの ROC の下の面積 (Area Under the Curve, AUC) が、0.7以上であればスクリーニングとして適すると判断する。
- 以下の方式で、最適なカットオフ値を求める (カッコ内は pROC の print.thres.best.method, OptimalCutpoints での methods, cutpointr の metric)
- 感度 + (1 - 特異度) が最大の点 (youden, Youden, youden)
- 左上からの距離が最小の点 (closest.topleft, ROC01, roc01)
- 感度 \(\times\) 特異度が最大の点 (…, MaxProdSpSe, prod_sens_spec)
- その他多数(CRANパッケージ内の説明を参照)
最適なカットオフ値の求め方については、どれが良いかは基準があまりないようです。また、近年でも他の方法も提案されています。
Unal I (2017) Defining an optimal cut-point value in ROC analysis: an alternative approach. Computational and Mathematical Methods in Medicine, 2017.
3.5 論文 Chakraborty (2021) PLoS One
Chakraborty S, Bhatia T, Sharma V, Antony N, Das D, Sahu S, … & Deshpande SN (2021) Psychometric properties of a screening tool for autism in the community—The Indian Autism Screening Questionnaire (IASQ). PLoS One, 16(4), e0249970. https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0249970
著者は13人いて、10人がニューデリーの機関に所属、3人は米国 Pittsuburgh の大学及び大学病院所属。
Its prevalence ranges from 0.15% to 1.01% depending on the screening method used [2–5]. (p. 1)
自閉症スペクトラム障がいの検査には時間がかかり、また検査ができるようにするための訓練にも時間がかかります。さらに、現状では乳幼児を対象にしたものがほとんどで、成人などを対象としたスクリーニングツールがありませんでした。一般に、自閉症の有病率は1〜2%と言われていますが、インドにおける先行研究ではこれより低い値で、著者らはスクリーニングツールにも問題があるのではないかという疑問があったようです。
筆者らは、2009年に40項目、5段階のツールを作りました (ISAA、40〜200点)。しかし、これはまだ検査者にトレーニングを要するなど、使いやすいものではありません。そこで、現在使われている検査の中から10の質問項目を抽出し、簡単にできるものを開発しました (IASQ、0〜10点)。このツールが有効であるかどうかを研究した論文です。
Participants on whom the tool was tested were parents/caregivers of individuals with autism or other psychiatric disorders clinically diagnosed by the treating clinician (gold standard), the autism individual being aged between 3–18 years with no comorbid physical or psychiatric disorder. (p. 4)
研究参加者は、自閉症または他の精神障害を診断されている、3〜18歳の人の親または介護者。
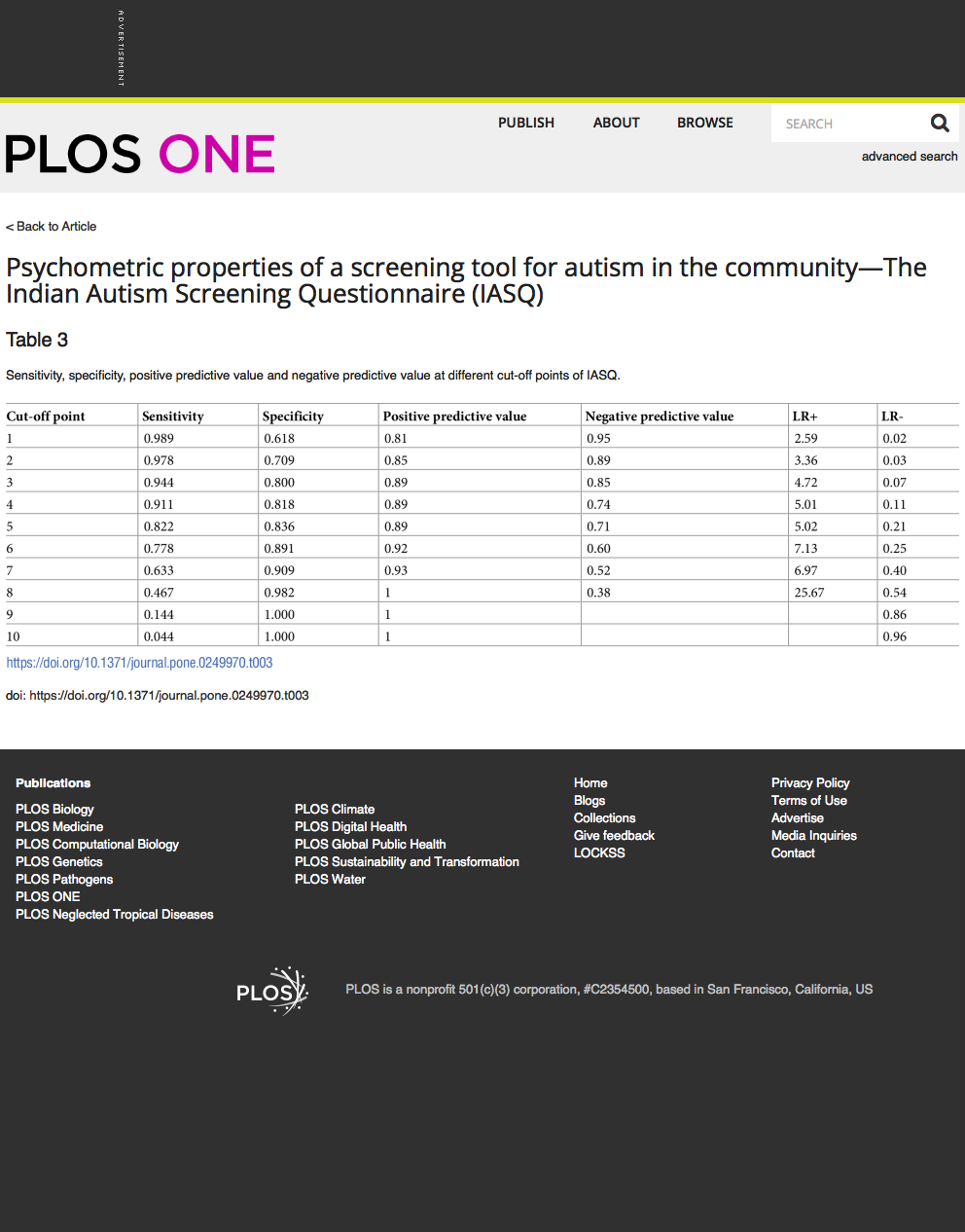
At a cutoff of 1, sensitivity was 99%, specificity 62%, PPV 81%, NPV 95%.
At a cutoff of 2, these values were 98%, 71%, 85% and 89% respectively. Calculating positive and negative likelihood ratios, either cutoff (1 or 2) were acceptable, depending on the aim.
カットオフ値を1とすると感度99%、特異度62%。カットオフ値を2とすると感度98%、特異度71%です。
During a subsequent ICMR Review Meeting (September 2019), whether to adopt 1 or 2 as cutoff was extensively discussed.
カットオフ値は、最終的に1としたようです。これはつまり、10項目中1項目でも当てはまれば、自閉症の可能性があるということになります。スクリーニングツールとしては、カットオフ値1点というのはどうなのか?とも思いますが、インドでは現状自閉症の可能性のある人を十分診断できていないという問題点から、低めに設定したと思われます。
3.6 Rパッケージ
ROC 曲線を描く CRAN パッケージ はたくさんあります。 その中で、カットオフ値を求めるものは、以下の3つになります。
- pROC
- OptimalCutpoints
- cutpointr
3.7 xlsx データの読み込み
まず、エクセルデータを読み込みます。 Rではインターネット上のデータをそのまま読み込むことができますが、エクセルの場合は拡張子 (.xls または .xlsx) が分からないときなどは .xls 形式と判断してしまいます。 このため、いったんダウンロードしてから開いています。 また、列名がかなり長く空白が含まれているので、後の処理のために新たに単純な列名の列を作ります。
library(curl)
library(readxl)
#curl_download("https://doi.org/10.1371/journal.pone.0249970.s005", "data/ROC.xlsx")
dfCutpoint <- read_excel("data/ROC.xlsx")## New names:
## • `Family ID` -> `Family ID...2`
## • `Family ID` -> `Family ID...10`dfCutpoint$Autism <- dfCutpoint$`Clinical Diagnosis of child autism 1, no autism 0`
dfCutpoint$IASQ <- dfCutpoint$`Total Score of IASQ`3.8 pROC
まずは、基本的な pROC ライブラリを試してみます。
library(pROC)
dfCutpoint$Autism <- as.factor(dfCutpoint$Autism)
plot.roc(dfCutpoint$Autism, dfCutpoint$IASQ)## Setting levels: control = 0, case = 1## Setting direction: controls < cases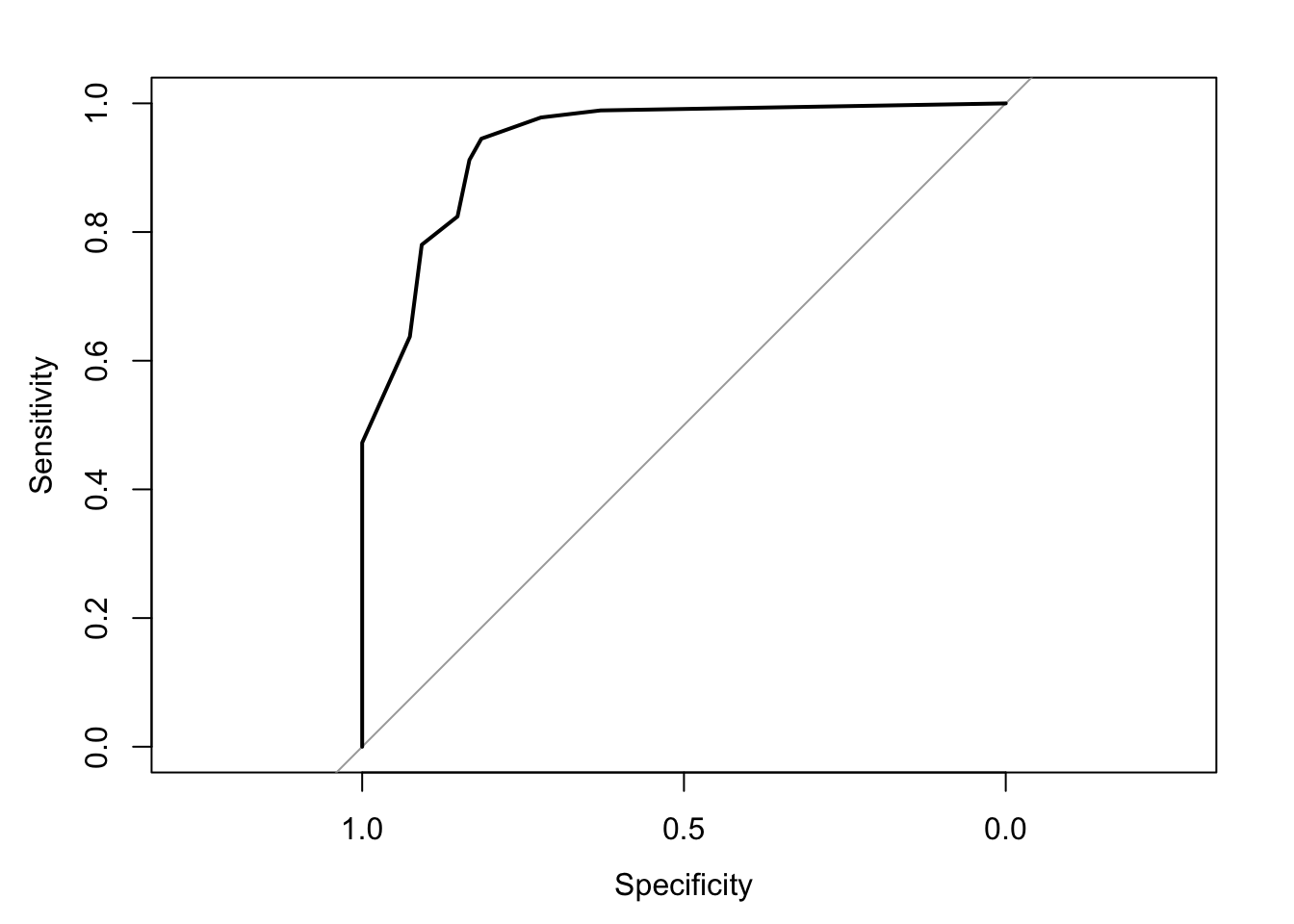
rocCutoff <- pROC::roc(response = dfCutpoint$Autism,
predictor = dfCutpoint$IASQ,
data = dfCutpoint)## Setting levels: control = 0, case = 1
## Setting direction: controls < casesROC曲線は描くことができました。しかし、x軸、y軸の範囲など直すところが多そうです。
次に、カットオフ値を求めます。
dfCutpoint$IASQ <- as.integer(dfCutpoint$IASQ)
coCutoff <- coords(roc = rocCutoff,
x = "best",
best.method = "youden")
datatable(coCutoff)結果が 2.5 となりました。 IASQはこの数値は小数点のある Double 型だったためと思われ 、整数 (integer) 型にしてみましたが、それでも代わりませんでした。 この時の感度が0.81、特異度が0.95と推定されました。
3.9 cutpointr
次に、cutpointr ライブラリを使います。
3.9.1 カットオフ値の決定
ここでは、Youden index が最大になる方法でカットオフ値を求めます。
主な引数の値
- metric:
- youden: Youden index (感度 + 特異度 - 1)
- sum_sens_spec: 感度 + 特異度
- prod_sens_spec: 感度 \(\times\) 特異度
- method:
- maximize_metric: metric を最大化します。
library(cutpointr)
cpROC <- cutpointr(data = dfCutpoint,
x = IASQ,
class = Autism,
method = maximize_metric,
metric = youden)## Assuming the positive class is 1## Assuming the positive class has higher x values3.9.2 カットオフ値の表示
結果を見てみます。
summary(cpROC)## Method: maximize_metric
## Predictor: IASQ
## Outcome: Autism
## Direction: >=
##
## AUC n n_pos n_neg
## 0.9383 145 91 54
##
## optimal_cutpoint youden acc sensitivity specificity tp fn fp tn
## 3 0.7599 0.8966 0.9451 0.8148 86 5 10 44
##
## Predictor summary:
## Data Min. 5% 1st Qu. Median Mean 3rd Qu. 95% Max. SD NAs
## Overall 0 0.0 1 6 4.710345 8 9 10 3.395089 0
## 0 0 0.0 0 0 1.314815 2 7 7 2.230357 0
## 1 0 2.5 6 7 6.725275 8 9 10 2.119046 0この場合、カットオフ値は3となりました。 この時の感度は0.9451、特異度は0.8148です。 ROC曲線の AUC は 0.9383 です。
なお、元の論文では、AUC は0.95、カットオフ値3 では、感度0.944、特異度0.800となっており、わずかですが数値が異なります。
3.10 OptimalCutpoint
OptimalCutpoints ライブラリのほうが、機能が多そうです。
López RM, Rodríguez ÁMX, Cadarso SCM, & Gude SF (2014) OptimalCutpoints: an R package for selecting optimal cutpoints in diagnostic tests. American Statistical Association. https://doi.org/10.18637/jss.v061.i08
引数
- tag.healty: 目的変数 (Autism) で、健康を示す値。
- methods
- “Youden”: Youden index (感度 + 特異度 - 1)
- “MaxSp”: 特異度を最大化
- control: 様々な制限をつけることができます。
- control.cutpoints(valueSe=0.95)
医学以外では、tag.healty の healthy という単語が馴染まないこともあるかと思います。
しかし、このデータではエラーが発生します。現在調査中です。 どうやら、IASQ = 8 など、全てが 1 になっているときにエラーが発生しているようです。
library(OptimalCutpoints)
dfCutpoint1 <- dfCutpoint[,c("IASQ", "Autism")]
ocROC <- optimal.cutpoints(
X = "IASQ",
status = "Autism",
data = dfCutpoint1,
tag.healthy = 0,
methods = "Youden",
control = control.cutpoints())エラー: Can’t subset columns that don’t exist.
x Locations 2, 6, 8, 11, 3, etc. don’t exist.
ℹ There are only 1 column.
Run rlang::last_error() to see where the error occurred.
3.13 サンプルサイズ
感度・特異度やROC曲線による解析は、サンプルサイズ計算はあまりされていないようです。 ただし、R で計算を行うことも可能ですので、研究計画に盛り込んでおくと良いでしょう。
サーバー側で R を使ってサンプルサイズ計算ができるサイトがあります。 このサイトでは、必要な引数を設定することで、R コードも表示されます。
https://shiny.ctu.unibe.ch/app_direct/presize/
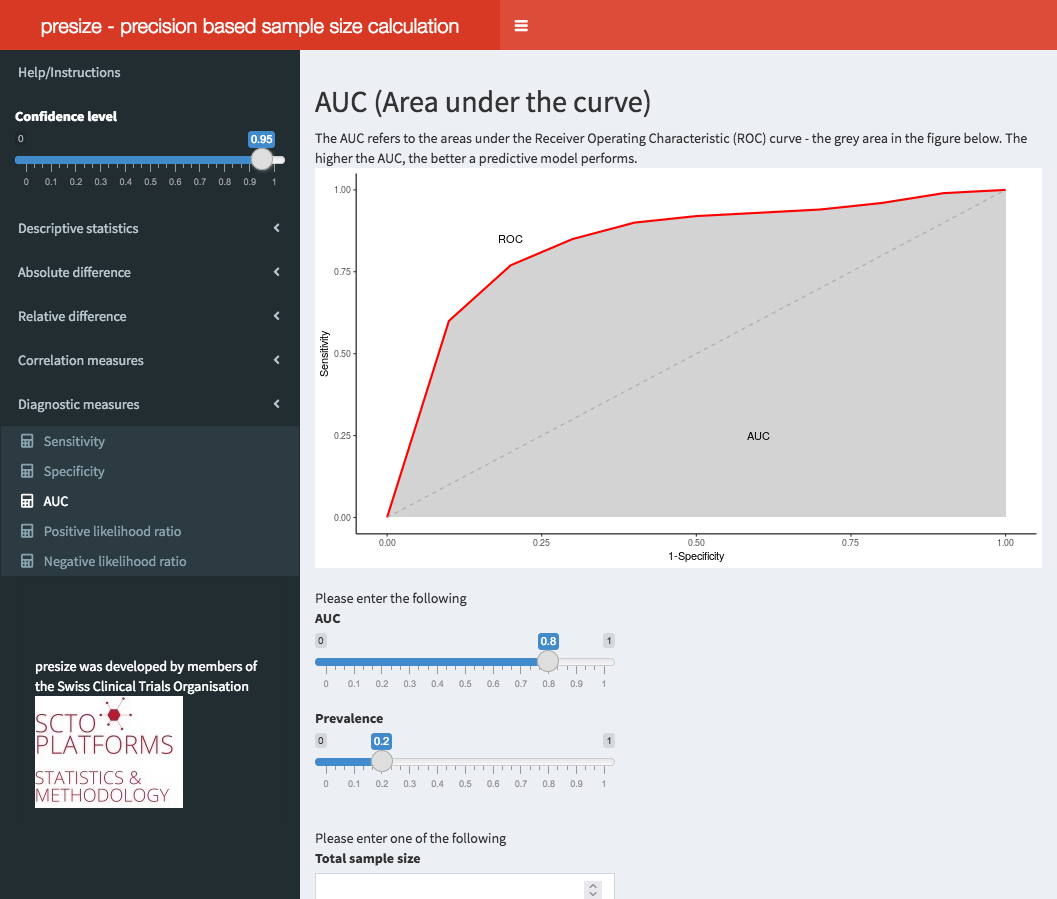
たとえば、感度 0.8、その95%信頼区間の幅を 0.1 (0.75-0.85) とする場合、 n = 244.154 が必要であることが示されます。
library(presize)
prec_sens(sens = 0.8, conf.width = 0.1, conf.level = 0.95, round = 'ceiling', method = 'wilson')##
## sample size for a sensitivity with Wilson confidence interval.
##
## sens sensadj n prev ntot conf.width conf.level lwr upr
## 1 0.8 0.795353 244.154 NA NA 0.1 0.95 0.745353 0.845353
##
## NOTE: sensadj is the adjusted sensitivity, from which the ci is calculated.Brown LD, Cai TT, DasGupta A (2001) Interval Estimation for a Binomial Proportion, Statistical Science , 16:2, 101-117, doi:10.1214/ss/1009213286
Bujang, M. A., & Adnan, T. H. (2016). Requirements for minimum sample size for sensitivity and specificity analysis. Journal of clinical and diagnostic research: JCDR, 10(10), YE01.