Chapter 5 生存曲線

5.1 生存時間解析

時間の経過の中で、あることが｛起こる・起こらない｝ということを調べるために、カプラン・マイヤー曲線を用います。この時、黄砂がある場合には

カプラン・マイヤー曲線の作図
検定
- log-rank 検定 (または一般化 Wilcoxon 検定)
- Cox 比例ハザードモデル

検定は、２群の比較しかできません。また、カプラン・マイヤー曲線が交差する場合は、検定する前に原因を見つける必要があります。

5.2 論文 Dessu (2020) PLoS One

Dessu S, Habte A, & Mesele M (2020). The Kaplan Meier estimates of mortality and its predictors among newborns admitted with low birth weight at public hospitals in Ethiopia. PloS one, 15(9), e0238629. https://doi.org/10.1371/journal.pone.0238629

新生児のうち、2500グラム未満で生まれる事例が全世界で毎年2000万件を超えています。2500グラム未満では免疫系が十分に発達しておらず、死亡リスクが高い状態にあります。

カプランマイヤー図は３つあります。

Fig 1:エピオピアの公立病院における2500グラム未満児の生存曲線
Fig 2:１時間以内に Kangaroo Mother Care (KMC) を開始した群とそうでない群
Fig 3:１時間以内に exclusive breast feeding を開始した群とそうでない群

ここでは、Fig 2を再現してみましょう。

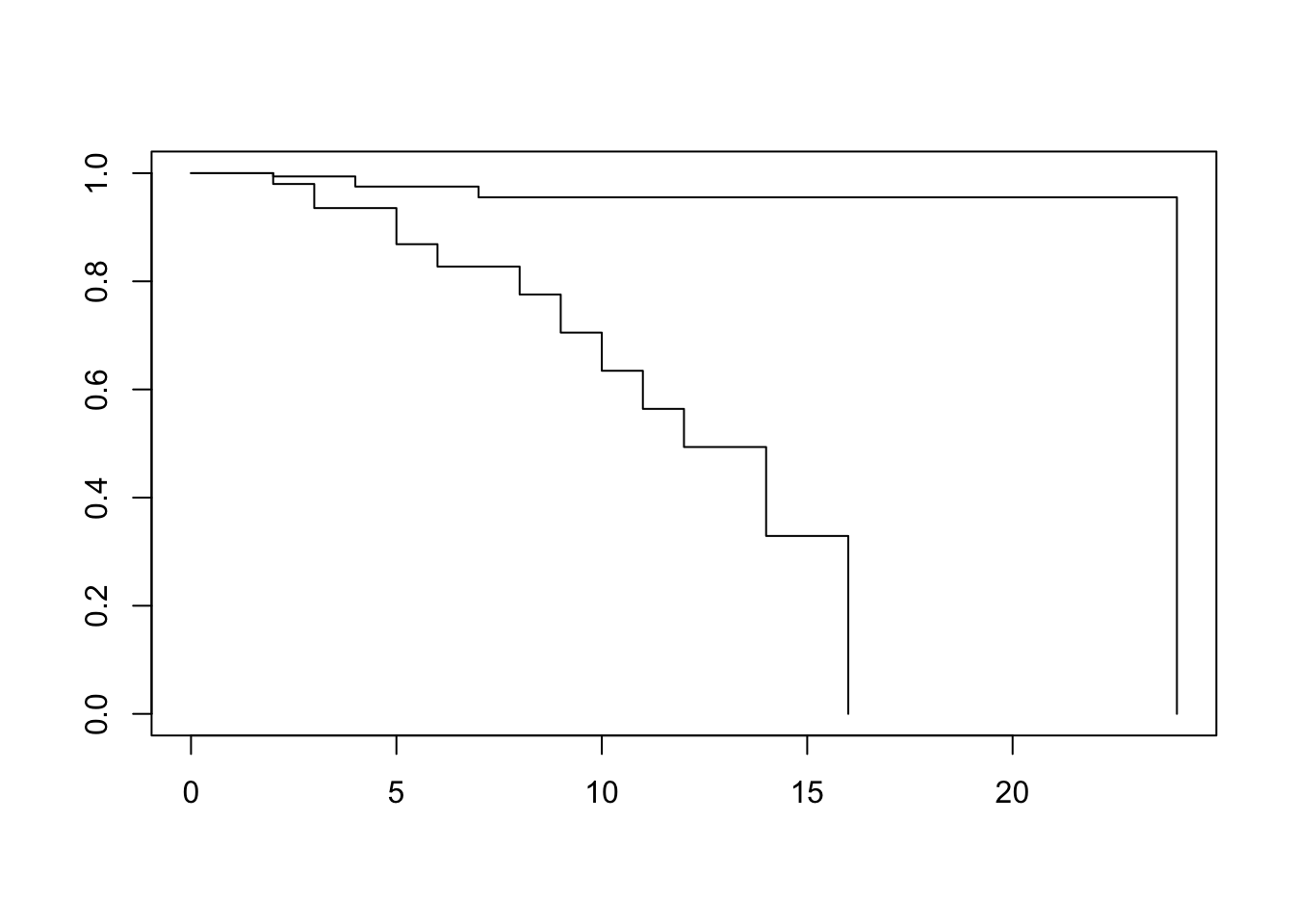
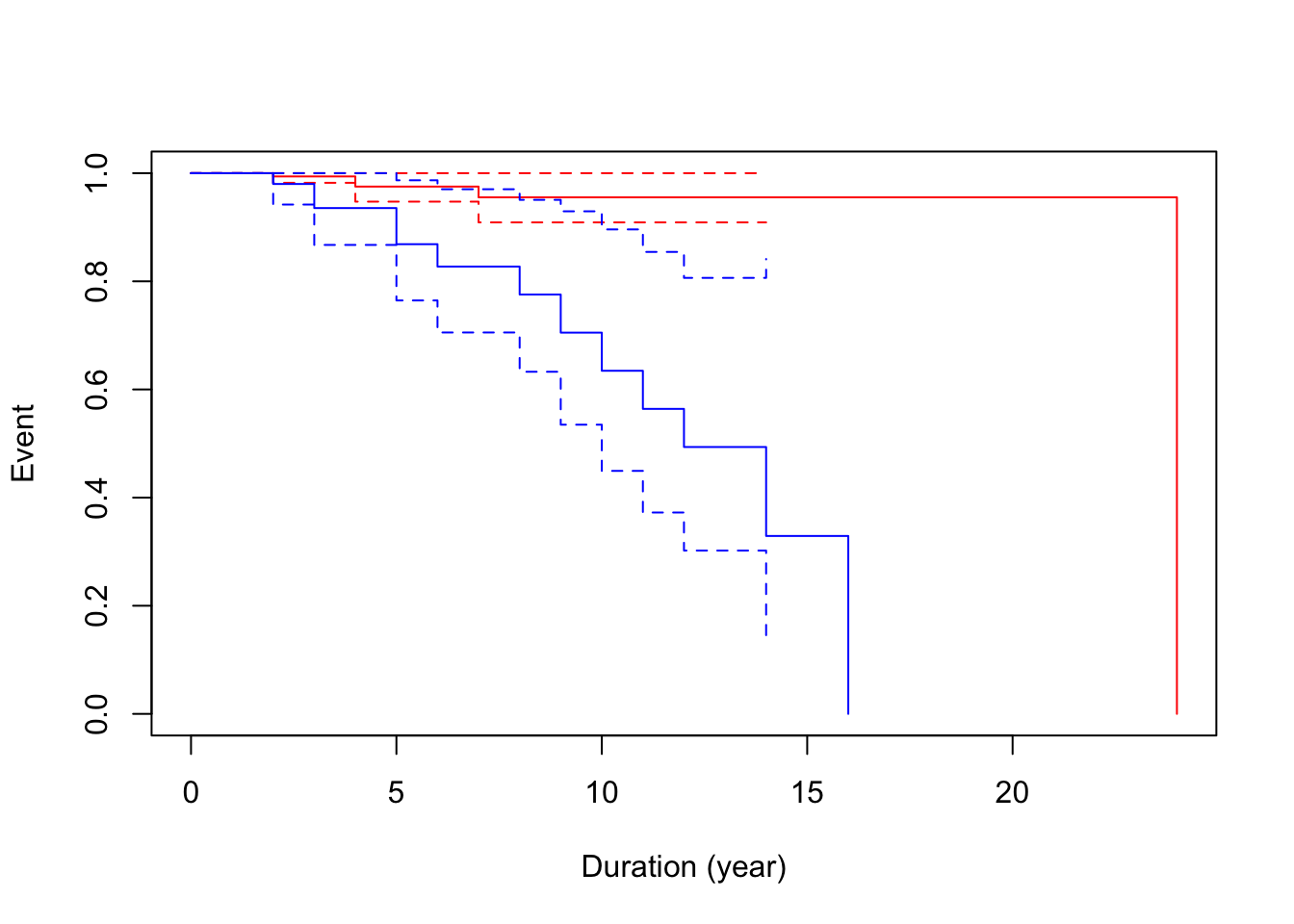
knitr::include_graphics("img/pone.0238629.g002.PNG_L.png")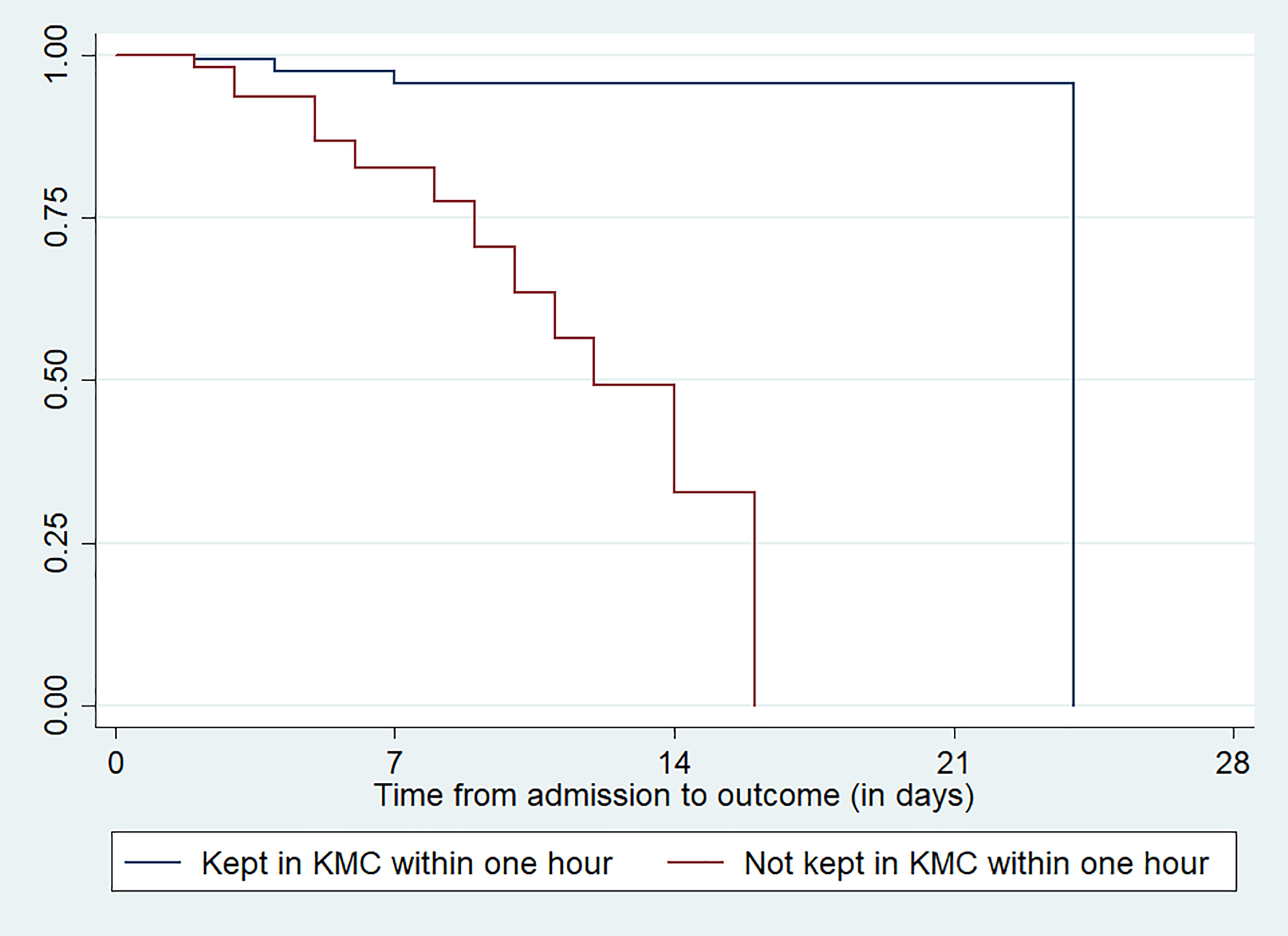

Dessu (2020) Fig 2. Survival estimation of neonates admitted with low birth weight for the variable kept the neonates in KMC within one hour at public hospitals in Ethiopia

Figure 5.1: Dessu (2020) Fig 2. Survival estimation of neonates admitted with low birth weight for the variable kept the neonates in KMC within one hour at public hospitals in Ethiopia

5.3 STATA データの読み込み

データを読み込みます。

library(haven)
dfSurvival <- read_stata("https://doi.org/10.1371/journal.pone.0238629.s001")
dfSurvival$KMC <- as.factor(dfSurvival$KMC)

生存分析の統計に先立ち、オブジェクトを準備します。

library(survival)
objSurv <- survfit(formula = Surv(stime,Died) ~ KMC, 
            data = dfSurvival)
summary(objSurv)

## Call: survfit(formula = Surv(stime, Died) ~ KMC, data = dfSurvival)
## 
##                 KMC=1.00 
##  time n.risk n.event survival std.err lower 95% CI upper 95% CI
##     2    165       1    0.994 0.00604        0.982            1
##     4    106       2    0.975 0.01441        0.947            1
##     7     49       1    0.955 0.02423        0.909            1
##    24      1       1    0.000     NaN           NA           NA
## 
##                 KMC=2.00 
##  time n.risk n.event survival std.err lower 95% CI upper 95% CI
##     2     50       1    0.980  0.0198        0.942        1.000
##     3     44       2    0.935  0.0361        0.867        1.000
##     5     28       2    0.869  0.0565        0.765        0.987
##     6     21       1    0.827  0.0673        0.705        0.970
##     8     16       1    0.776  0.0805        0.633        0.951
##     9     11       1    0.705  0.0994        0.535        0.929
##    10     10       1    0.635  0.1117        0.449        0.896
##    11      9       1    0.564  0.1195        0.372        0.854
##    12      8       1    0.494  0.1236        0.302        0.806
##    14      3       1    0.329  0.1576        0.129        0.841
##    16      1       1    0.000     NaN           NA           NA

変数

objSurv: survival パッケージのオブジェクト。
dfSurvival: 上で作ったデータフレーム。

関数

survfit: survival パッケージの関数。生存時間データのカプランマイヤー推定で用いる関数
Surv: survival パッケージの関数。生存時間データオブジェクトを作成する。
summary: base 関数。

5.4 生存曲線の作成

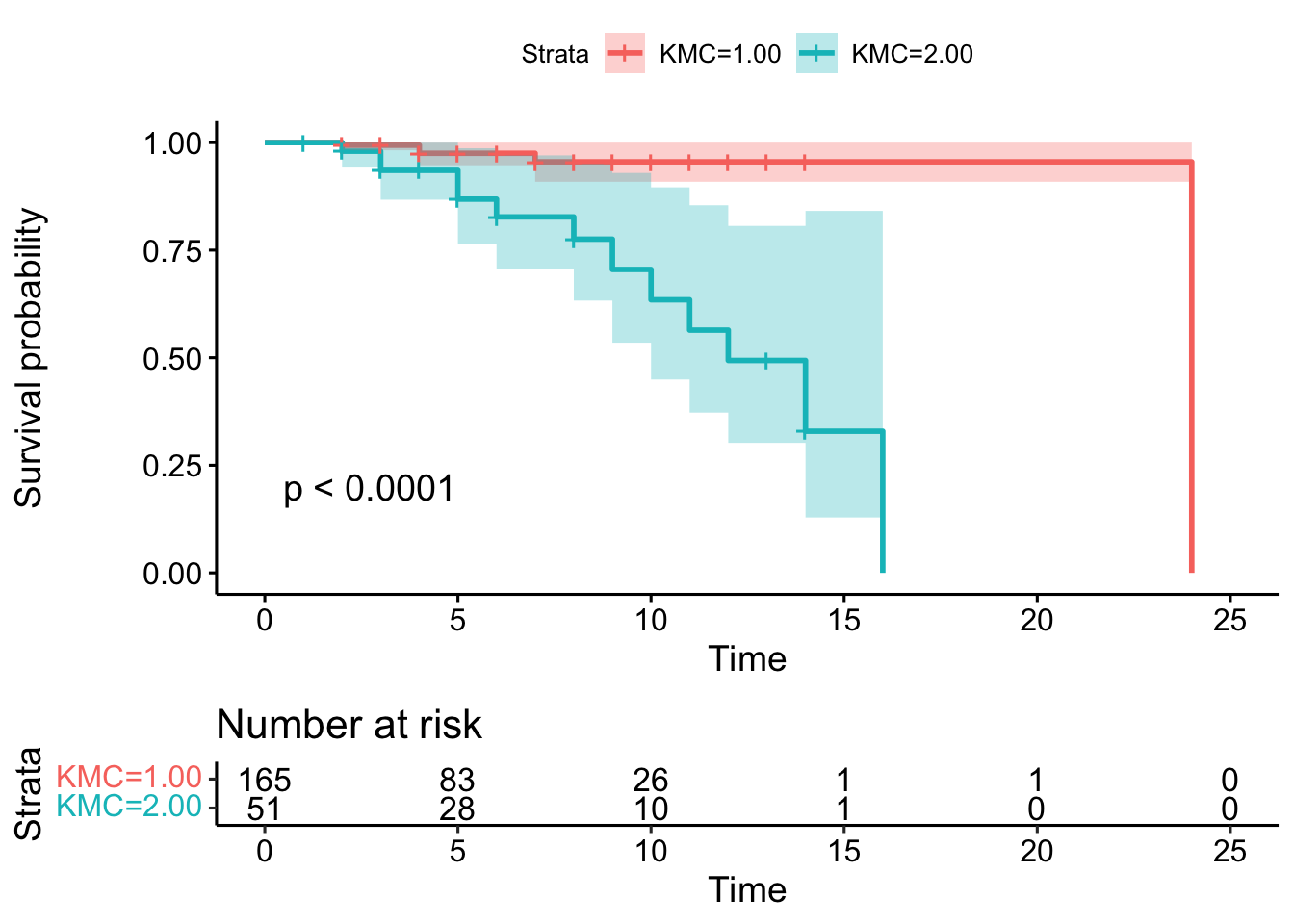
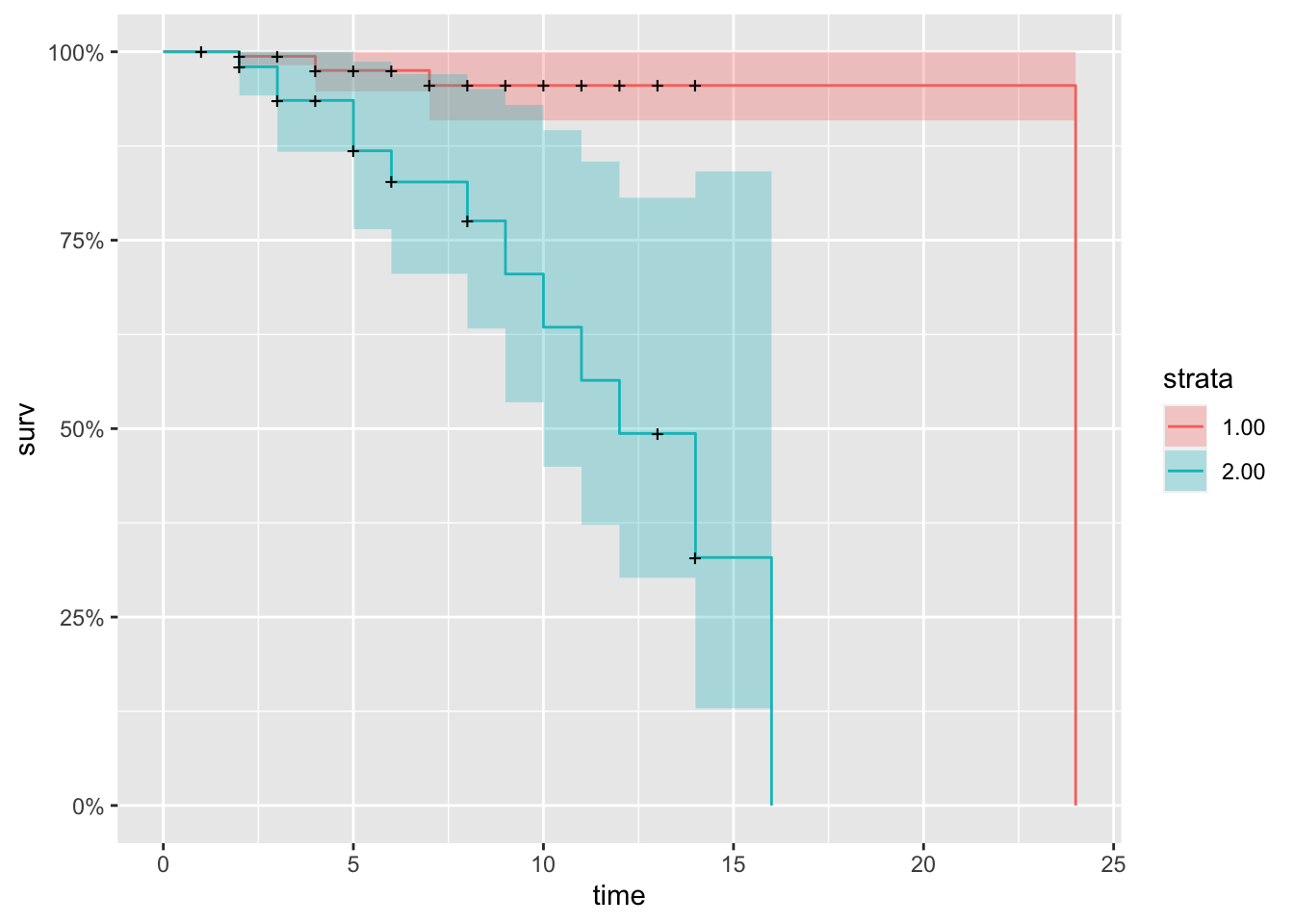
生存曲線 (Kaplan-Meier 曲線) を描いてみましょう。 R で作図する場合、大きく分けて base 関数の plot を用いる方法と、多機能な ggplot2 ライブラリを用いる方法があります。

5.4.1 plot

base 関数のplotで生存曲線を描くことができます。

plot(x = objSurv)

いろいろなオプションを試してみましょう。

plot(x = objSurv, 
            conf.int = T, 
            col = c("red","blue"), 
            xlab= "Duration (year)", 
            ylab = "Event")

5.4.2 ggplot2

ライブラリ survminer を使用します。

library(survminer)
ggsurvplot(fit = objSurv, 
            data = dfSurvival, 
            risk.table = TRUE, 
            pval = TRUE, 
            conf.int = TRUE, 
            risk.table.y.text.col = TRUE)

ライブラリ ggfortify を使用します。

library(ggfortify)
autoplot(objSurv, data = dfSurvival )

5.5 log-rank 検定

5.5.1 ２群の比較 log-rank 検定

ログ・ランク (log-rank)検定は、群ごとのイベントありとなしに集計したクロス表のカイ２乗検定です。R の survival パッケージが自動的に計算します。

survdiff(Surv(stime,Died)~KMC, 
            data = dfSurvival)

## Call:
## survdiff(formula = Surv(stime, Died) ~ KMC, data = dfSurvival)
## 
##            N Observed Expected (O-E)^2/E (O-E)^2/V
## KMC=1.00 165        5    13.29      5.17      20.6
## KMC=2.00  51       13     4.71     14.57      20.6
## 
##  Chisq= 20.6  on 1 degrees of freedom, p= 6e-06

p < 0.01 なので、この場合は群間差があったと判断します。

5.6 サンプルサイズ

library(powerSurvEpi)
library(npsurvSS)
library(gsDesign)

5.6.1 Log-Rank 検定

5.6.2 Cox 比例ハザードモデル

powerSurvEpi
npsurvSS
gsDesign

ライブラリ powerSurvEpi は、パイロット試験データを元に、Cox 比例ハザードモデルのサンプルサイズ計算を行うことができます。

library(powerSurvEpi)
dfSurvival$KMC2 <- factor(x = dfSurvival$KMC, levels = c("1.00", "2.00"), labels = c("C", "E"))
samplesize <- ssizeCT(formula = Surv(stime,Died) ~ KMC2, 
        dat = dfSurvival,
        power = 0.80,
        k = 1,
        RR = 1.2,
        alpha = 0.05)

関数

factor 因子型の列を作成します。元となる列はKMCで、値 (“1.00”, “2.00”) を (“C”, “E”) に割り当てています。

引数	内容
formula	これまでも使って来た式です。目的変数は Surv 関数を使う必要があります。説明変数は、“C” と “E” からなる因子型である必要があります。
k	暴露群:対照群の比率 (k:1) です。
RR	ハザード比の仮定値です。