Chapter 5 Risk Ratio

5.1 はじめに

Davis and Weller (2021) の論文からデータを用いる。

スタチン療法は多くの循環器系の疾患を減少させることが知られている。一方で、スタチン関連の筋症状のためアドヒアランスが低く、結果として循環器系アウトカムの低下に繋がっている可能性がある。さらに、スタチンの量とも関係していることが予想されるが、量の多い (high intensity) スタチン療法の研究は少ない。そのため、ネットワークメタ分析で、placebo-moderate, moderato-high, placebo-high の比較を行った。

5.1.1 データ読み込み

arm-based と contrast-based データをあらかじめ読み込む。それぞれ、データフレーム名は dfArm と dfCon とする。

library(readxl)
dfArm <- read_excel("data/RR.xlsx", sheet = "arm")
dfCon <- read_excel("data/RR.xlsx", sheet = "contrast")

5.2 頻度論 netmeta

5.2.1 データ

arm-based から読み込む場合は、以下のようになる。

dfNetMeta <- pairwise(
  treat = treat, 
  event = X, 
  n = Total, 
  studlab = Study, 
  data = dfArm, 
  sm ="RR")
netmetaDavis <- netmeta(TE, seTE, treat1, treat2, studlab, data = dfNetMeta, sm="RR", reference="Placebo")

contrast-based データの場合は、以下のようになる。なお、treat1 = treat1 の左側の treat1 は、この関数の引数名である。右側の treat1 は、エクセル中の列名（データフレームの列名）である。

netmetaShim <- netmetabin(
  treat1 = treat1, 
  treat2 = treat2, 
  n1 = n1, 
  n2 = n2, 
  event1 = event1, 
  event2 = event2, 
  studlab = study, 
  data=dfCon, 
  sm="RR", 
  reference="Placebo")

Xie 2016 が削除された。おそらくイベント数が0のものがあるためだろうか？arm-based データを pairwise() で計算すると、event = 0 を +0.5 して OR を計算するので、arm-based の方が良いかもしれない。

5.2.2 Network plot

netgraph(netmetaDavis, 
         plastic = FALSE,                    # 3Dではなくする
         points = TRUE,                      # ノードを表示する
         thickness = "number.of.studies",    # 線の太さを研究数にする
         multiarm = TRUE)                    # multiarm のところを塗りつぶす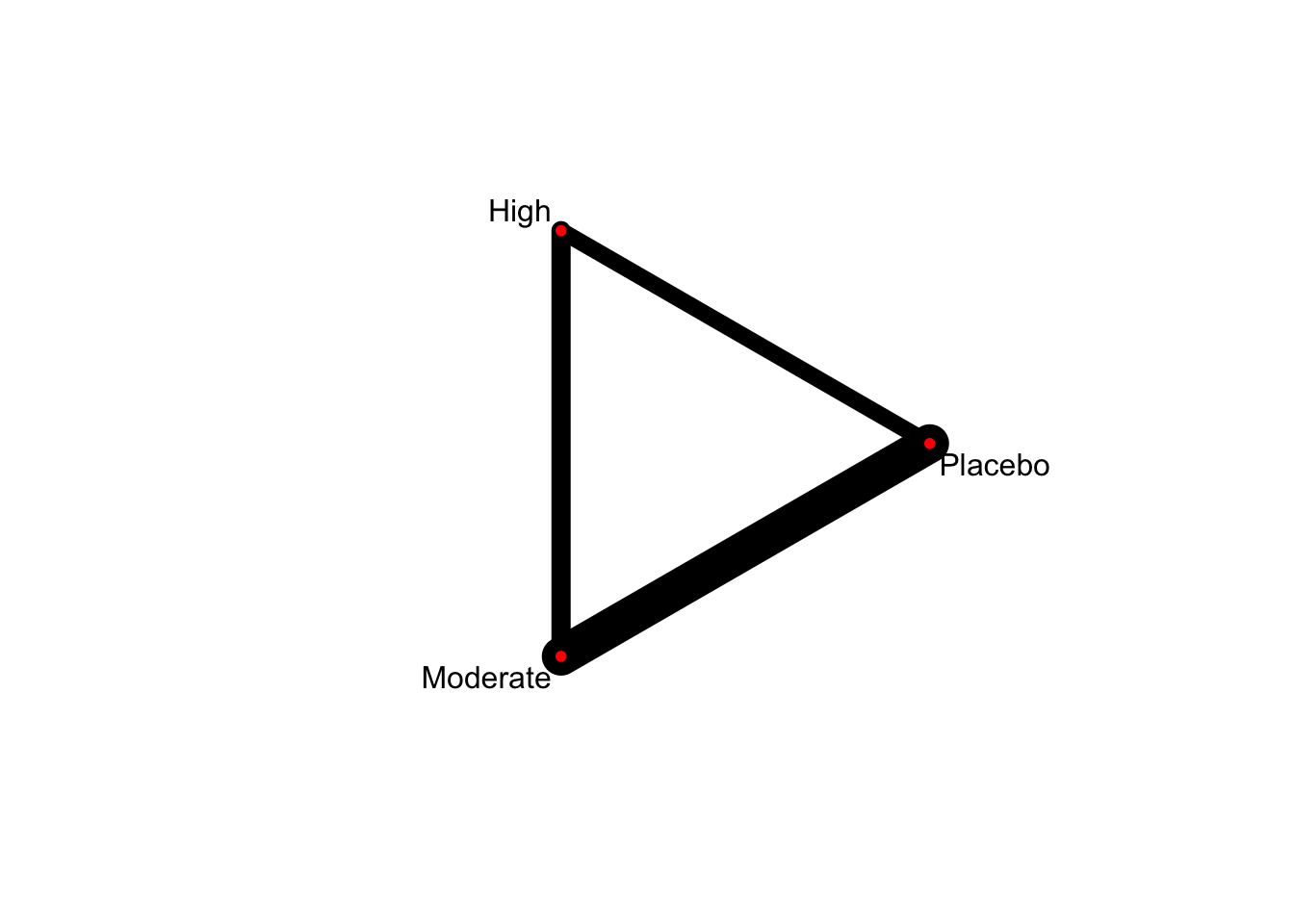

ノードの大きさを変更することはできない。

5.2.3 要約

summary(netmetaDavis)
## Original data:
## 
##                          treat1   treat2      TE   seTE
## 4D, A20                Moderate  Placebo  0.3636 0.5828
## A to Z, S40-S80 vs S20     High Moderate  0.1725 0.2300
## AFCAPS, L20-L40        Moderate  Placebo  0.0399 0.0197
## ALERT, F40-F80         Moderate  Placebo -0.0056 0.0433
## ASCOT, A10             Moderate  Placebo  0.0473 0.0806
## ASPEN, A10             Moderate  Placebo  0.6291 0.2806
## AURORA, R10            Moderate  Placebo -0.1091 0.0685
## CARDS, A10             Moderate  Placebo -0.0167 0.0512
## CARE, P40              Moderate  Placebo -2.1958 1.4904
## CORONA,R10             Moderate  Placebo  0.0766 0.0921
## GISSI-HF, R10          Moderate  Placebo  0.0927 0.3004
## HOPE, R10              Moderate  Placebo  1.0945 1.1544
## HPS, S40               Moderate  Placebo -0.0090 0.0199
## JUPITER, R20               High  Placebo  0.0323 0.0347
## LIPID, P40             Moderate  Placebo -0.2254 0.4739
## PROSPER, P40           Moderate  Placebo  0.1254 0.2415
## PROVE-IT, A80 vs P40       High Moderate  0.1915 0.1772
## SEARCH, S80 vs S20         High Moderate  0.0428 0.0212
## SPARCL, A80                High  Placebo -0.0885 0.1183
## SSSS, S20-S40          Moderate  Placebo  0.0358 0.0492
## TNT, A80 vs A10            High Moderate  0.0317 0.0896
## TRACE RA, A40              High  Placebo  0.1166 0.1216
## WOSCOPS, P40           Moderate  Placebo -0.0530 0.1397
## 
## Number of treatment arms (by study):
##                        narms
## 4D, A20                    2
## A to Z, S40-S80 vs S20     2
## AFCAPS, L20-L40            2
## ALERT, F40-F80             2
## ASCOT, A10                 2
## ASPEN, A10                 2
## AURORA, R10                2
## CARDS, A10                 2
## CARE, P40                  2
## CORONA,R10                 2
## GISSI-HF, R10              2
## HOPE, R10                  2
## HPS, S40                   2
## JUPITER, R20               2
## LIPID, P40                 2
## PROSPER, P40               2
## PROVE-IT, A80 vs P40       2
## SEARCH, S80 vs S20         2
## SPARCL, A80                2
## SSSS, S20-S40              2
## TNT, A80 vs A10            2
## TRACE RA, A40              2
## WOSCOPS, P40               2
## 
## Results (common effects model):
## 
##                          treat1   treat2     RR           95%-CI    Q leverage
## 4D, A20                Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.37     0.00
## A to Z, S40-S80 vs S20     High Moderate 1.0386 [1.0035; 1.0749] 0.34     0.01
## AFCAPS, L20-L40        Moderate  Placebo 1.0098 [0.9875; 1.0326] 2.33     0.33
## ALERT, F40-F80         Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.13     0.07
## ASCOT, A10             Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.22     0.02
## ASPEN, A10             Moderate  Placebo 1.0098 [0.9875; 1.0326] 4.87     0.00
## AURORA, R10            Moderate  Placebo 1.0098 [0.9875; 1.0326] 3.01     0.03
## CARDS, A10             Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.27     0.05
## CARE, P40              Moderate  Placebo 1.0098 [0.9875; 1.0326] 2.19     0.00
## CORONA,R10             Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.53     0.02
## GISSI-HF, R10          Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.08     0.00
## HOPE, R10              Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.88     0.00
## HPS, S40               Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.90     0.33
## JUPITER, R20               High  Placebo 1.0488 [1.0104; 1.0886] 0.19     0.30
## LIPID, P40             Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.25     0.00
## PROSPER, P40           Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.23     0.00
## PROVE-IT, A80 vs P40       High Moderate 1.0386 [1.0035; 1.0749] 0.75     0.01
## SEARCH, S80 vs S20         High Moderate 1.0386 [1.0035; 1.0749] 0.05     0.68
## SPARCL, A80                High  Placebo 1.0488 [1.0104; 1.0886] 1.32     0.03
## SSSS, S20-S40          Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.28     0.05
## TNT, A80 vs A10            High Moderate 1.0386 [1.0035; 1.0749] 0.00     0.04
## TRACE RA, A40              High  Placebo 1.0488 [1.0104; 1.0886] 0.32     0.02
## WOSCOPS, P40           Moderate  Placebo 1.0098 [0.9875; 1.0326] 0.20     0.01
## 
## Results (random effects model):
## 
##                          treat1   treat2     RR           95%-CI
## 4D, A20                Moderate  Placebo 1.0098 [0.9875; 1.0326]
## A to Z, S40-S80 vs S20     High Moderate 1.0386 [1.0035; 1.0749]
## AFCAPS, L20-L40        Moderate  Placebo 1.0098 [0.9875; 1.0326]
## ALERT, F40-F80         Moderate  Placebo 1.0098 [0.9875; 1.0326]
## ASCOT, A10             Moderate  Placebo 1.0098 [0.9875; 1.0326]
## ASPEN, A10             Moderate  Placebo 1.0098 [0.9875; 1.0326]
## AURORA, R10            Moderate  Placebo 1.0098 [0.9875; 1.0326]
## CARDS, A10             Moderate  Placebo 1.0098 [0.9875; 1.0326]
## CARE, P40              Moderate  Placebo 1.0098 [0.9875; 1.0326]
## CORONA,R10             Moderate  Placebo 1.0098 [0.9875; 1.0326]
## GISSI-HF, R10          Moderate  Placebo 1.0098 [0.9875; 1.0326]
## HOPE, R10              Moderate  Placebo 1.0098 [0.9875; 1.0326]
## HPS, S40               Moderate  Placebo 1.0098 [0.9875; 1.0326]
## JUPITER, R20               High  Placebo 1.0488 [1.0104; 1.0886]
## LIPID, P40             Moderate  Placebo 1.0098 [0.9875; 1.0326]
## PROSPER, P40           Moderate  Placebo 1.0098 [0.9875; 1.0326]
## PROVE-IT, A80 vs P40       High Moderate 1.0386 [1.0035; 1.0749]
## SEARCH, S80 vs S20         High Moderate 1.0386 [1.0035; 1.0749]
## SPARCL, A80                High  Placebo 1.0488 [1.0104; 1.0886]
## SSSS, S20-S40          Moderate  Placebo 1.0098 [0.9875; 1.0326]
## TNT, A80 vs A10            High Moderate 1.0386 [1.0035; 1.0749]
## TRACE RA, A40              High  Placebo 1.0488 [1.0104; 1.0886]
## WOSCOPS, P40           Moderate  Placebo 1.0098 [0.9875; 1.0326]
## 
## Number of studies: k = 23
## Number of pairwise comparisons: m = 23
## Number of treatments: n = 3
## Number of designs: d = 3
## 
## Common effects model
## 
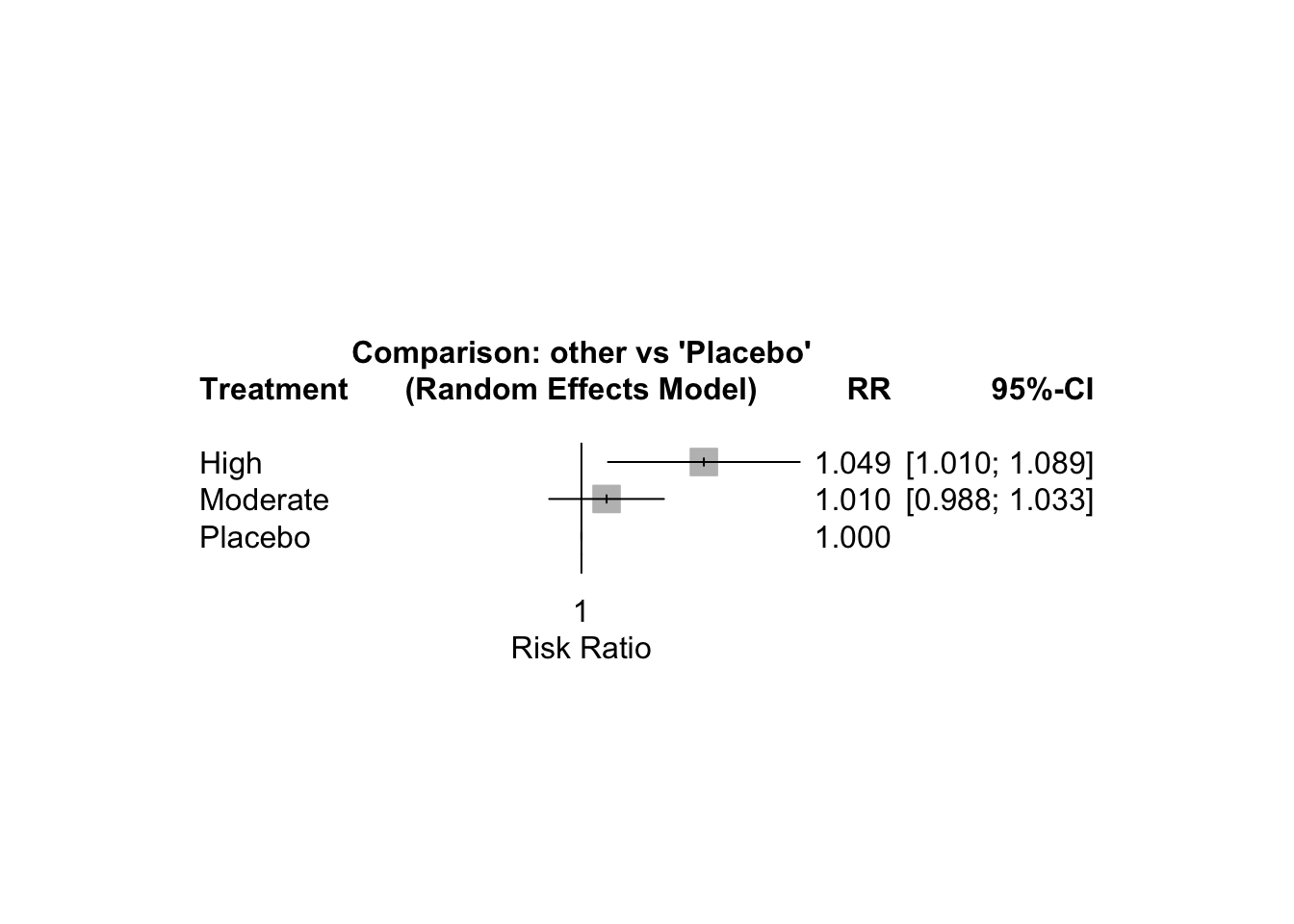
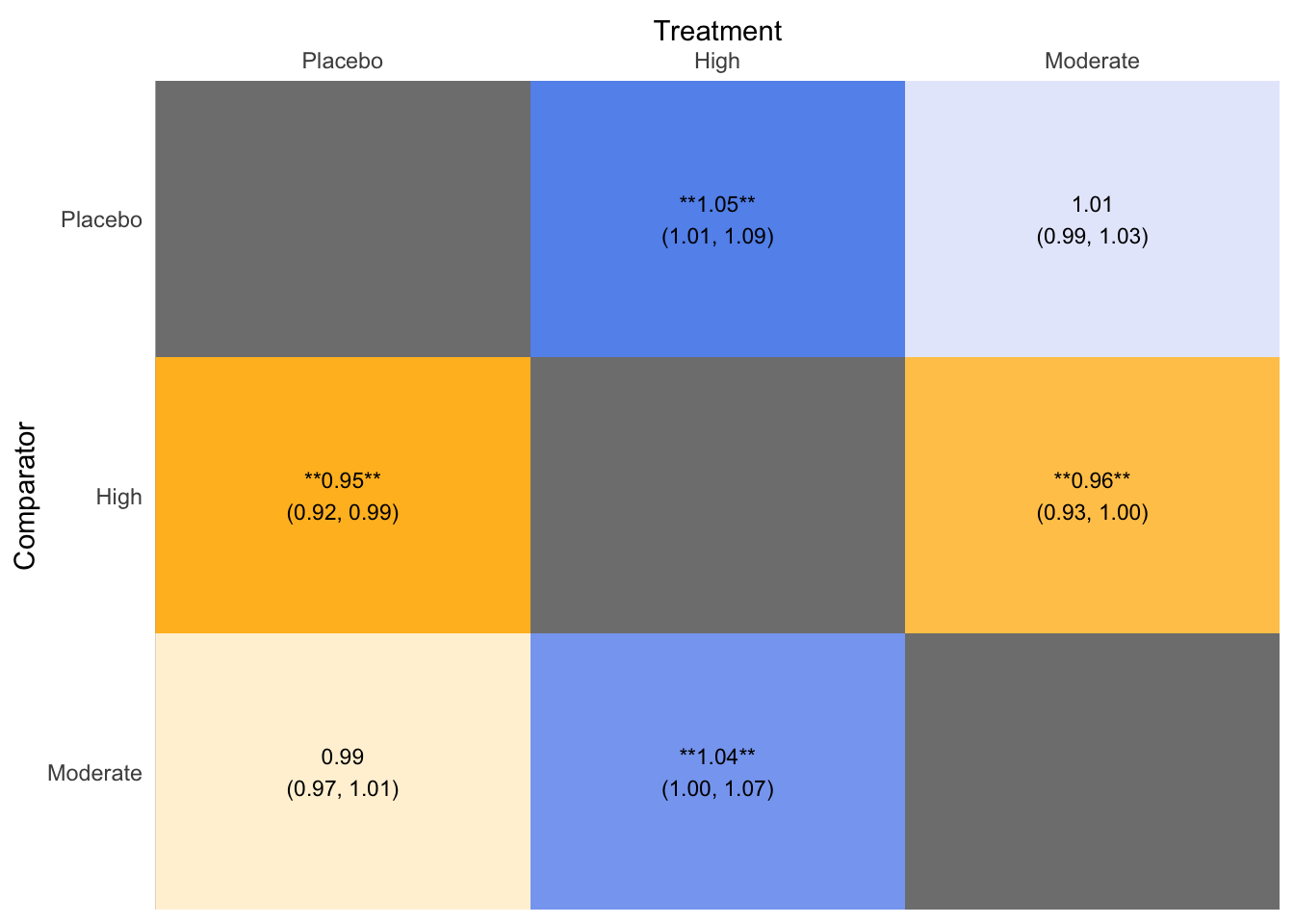
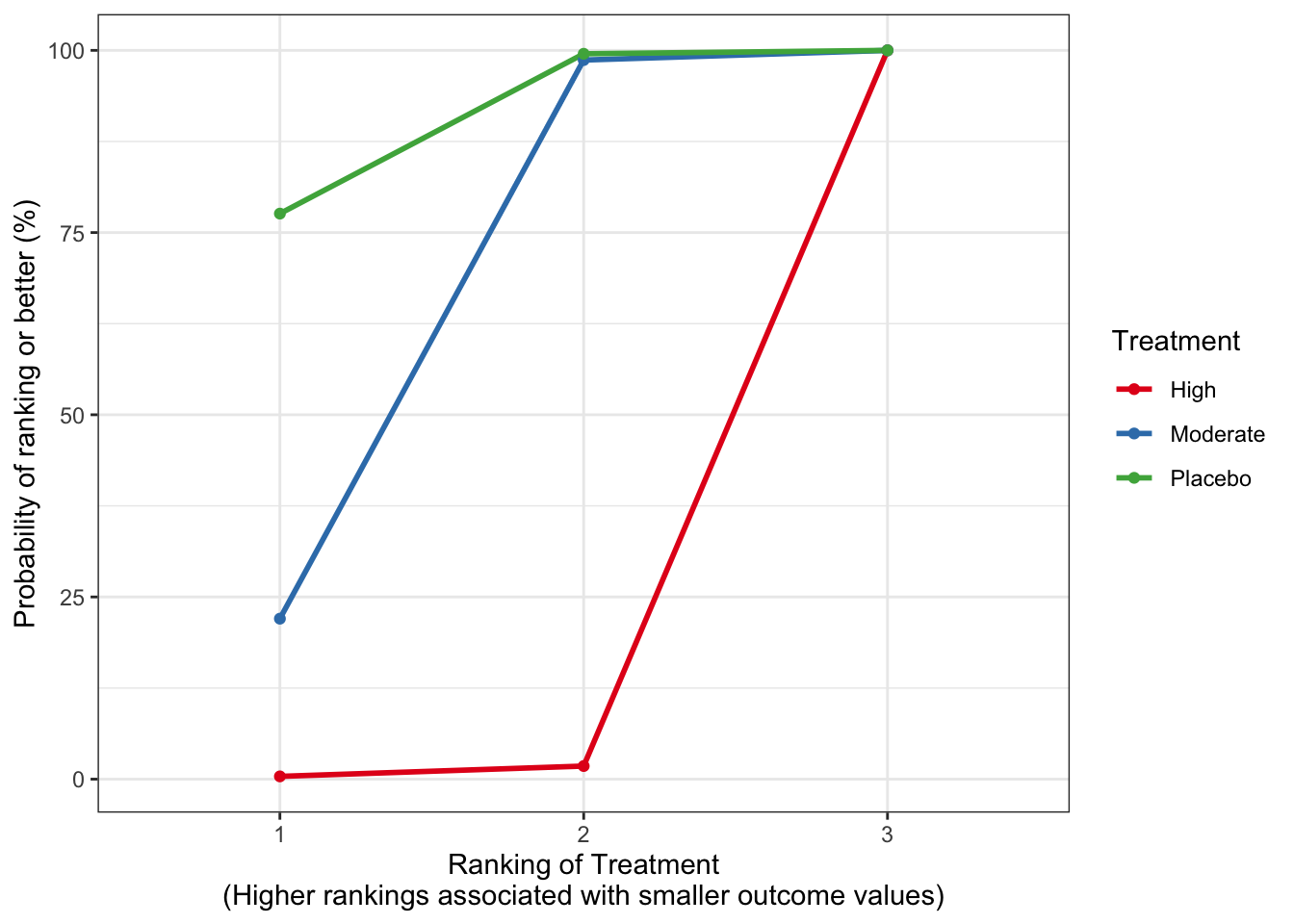
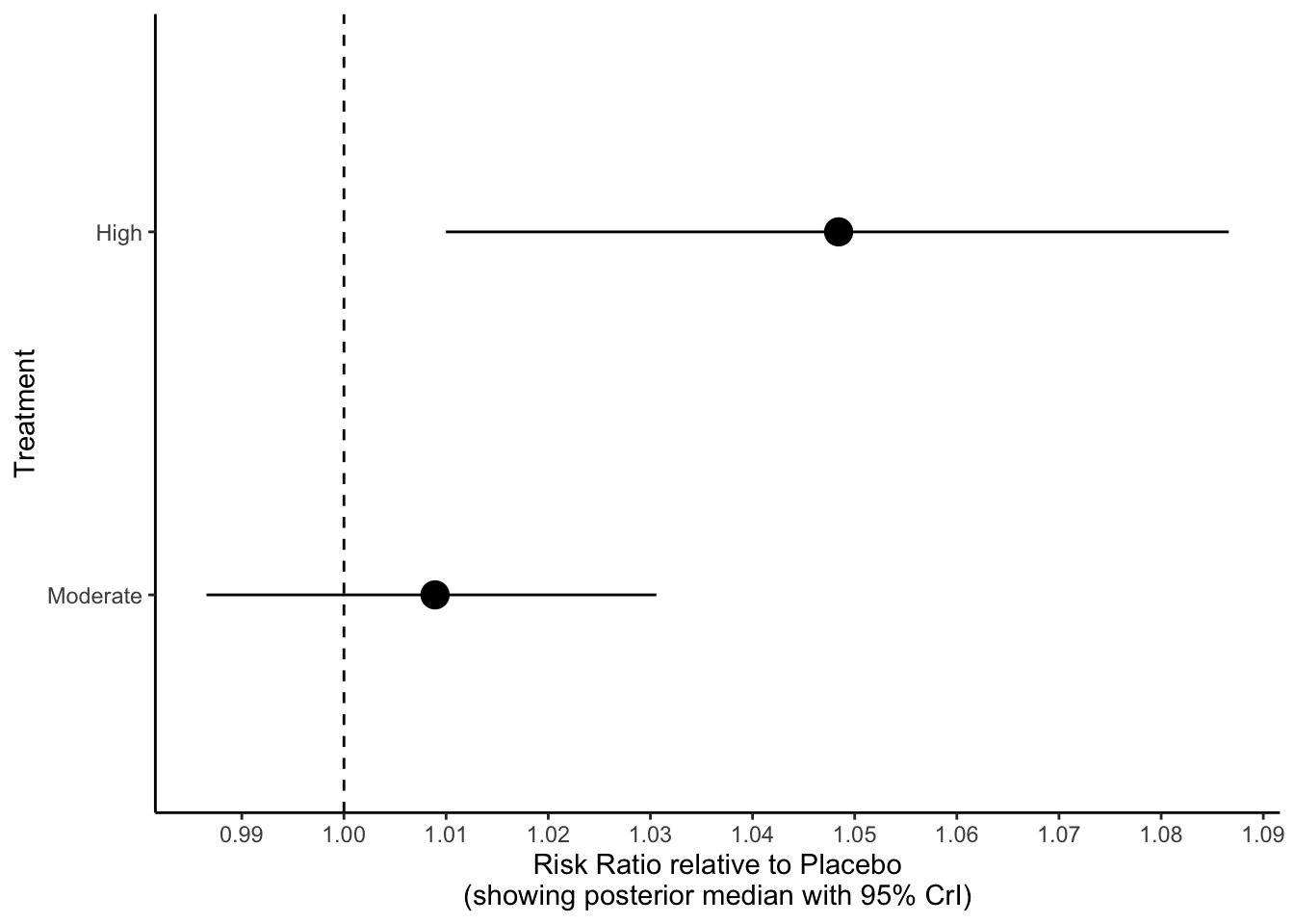
## Treatment estimate (sm = 'RR', comparison: other treatments vs 'Placebo'):
##              RR           95%-CI    z p-value
## High     1.0488 [1.0104; 1.0886] 2.50  0.0123
## Moderate 1.0098 [0.9875; 1.0326] 0.86  0.3904
## Placebo       .                .    .       .
## 
## Random effects model
## 
## Treatment estimate (sm = 'RR', comparison: other treatments vs 'Placebo'):
##              RR           95%-CI    z p-value
## High     1.0488 [1.0104; 1.0886] 2.50  0.0123
## Moderate 1.0098 [0.9875; 1.0326] 0.86  0.3904
## Placebo       .                .    .       .
## 
## Quantifying heterogeneity / inconsistency:
## tau^2 = 0; tau = 0; I^2 = 0% [0.0%; 46.2%]
## 
## Tests of heterogeneity (within designs) and inconsistency (between designs):
##                     Q d.f. p-value
## Total           19.71   21  0.5397
## Within designs  19.21   20  0.5082
## Between designs  0.50    1  0.4793

5.2.4 一貫性の評価

decomp.design(netmetaShim)
## Q statistics to assess homogeneity / consistency
## 
##                    Q df p-value
## Total           4.90 19  0.9995
## Within designs  4.68 15  0.9945
## Between designs 0.22  4  0.9942
## 
## Design-specific decomposition of within-designs Q statistic
## 
##              Design    Q df p-value
##  Placebo:IV(double) 1.89  7  0.9655
##  Placebo:IV(single) 1.96  6  0.9229
##     Placebo:Topical 0.82  2  0.6631
## 
## Between-designs Q statistic after detaching of single designs
## 
##                 Detached design    Q df p-value
##              IV(double):Topical 0.12  3  0.9897
##              Placebo:IV(double) 0.12  3  0.9897
##              Placebo:IV(single) 0.19  3  0.9798
##                 Placebo:Topical 0.10  3  0.9919
##  Combination:IV(single):Topical 0.21  2  0.9019
##  Placebo:Combination:IV(single) 0.13  2  0.9363
## 
## Q statistic to assess consistency under the assumption of
## a full design-by-treatment interaction random effects model
## 
##                    Q df p-value tau.within tau2.within
## Between designs 0.22  4  0.9942          0           0
print(netsplit(netmetaDavis), digits=3)
## Separate indirect from direct evidence (SIDE) using back-calculation method
## 
## Common effects model: 
## 
##        comparison  k prop   nma direct indir.   RoR     z p-value
##     High:Moderate  4 0.74 1.039  1.046  1.017 1.029  0.71  0.4793
##      High:Placebo  3 0.35 1.049  1.030  1.059 0.972 -0.71  0.4793
##  Moderate:Placebo 16 0.91 1.010  1.012  0.984 1.029  0.71  0.4793
## 
## Random effects model: 
## 
##        comparison  k prop   nma direct indir.   RoR     z p-value
##     High:Moderate  4 0.74 1.039  1.046  1.017 1.029  0.71  0.4793
##      High:Placebo  3 0.35 1.049  1.030  1.059 0.972 -0.71  0.4793
##  Moderate:Placebo 16 0.91 1.010  1.012  0.984 1.029  0.71  0.4793
## 
## Legend:
##  comparison - Treatment comparison
##  k          - Number of studies providing direct evidence
##  prop       - Direct evidence proportion
##  nma        - Estimated treatment effect (RR) in network meta-analysis
##  direct     - Estimated treatment effect (RR) derived from direct evidence
##  indir.     - Estimated treatment effect (RR) derived from indirect evidence
##  RoR        - Ratio of Ratios (direct versus indirect)
##  z          - z-value of test for disagreement (direct versus indirect)
##  p-value    - p-value of test for disagreement (direct versus indirect)

p < 0.05 であると、非一貫である。

5.2.5 Ranking

netrank(netmetaDavis, small.values="good")
##          P-score (common) P-score (random)
## Placebo            0.8993           0.8993
## Moderate           0.5899           0.5899
## High               0.0108           0.0108

5.2.6 Forest plot

library(metafor)
metafor::forest(netmetaDavis, ref="Placebo", digits=3, xlab="Risk Ratio")

5.3 gemtc ベイジアン

gemtc は、原則として arm-based データをとる。また、gemtc は、あらかじめ列名を指定の名称にしなければならない。

library(gemtc)

dfGemtc <- dfArm
colnames(dfGemtc) <- c("study", "responders", "sampleSize", "description")
dfGemtc$treatment <- dfArm$treat
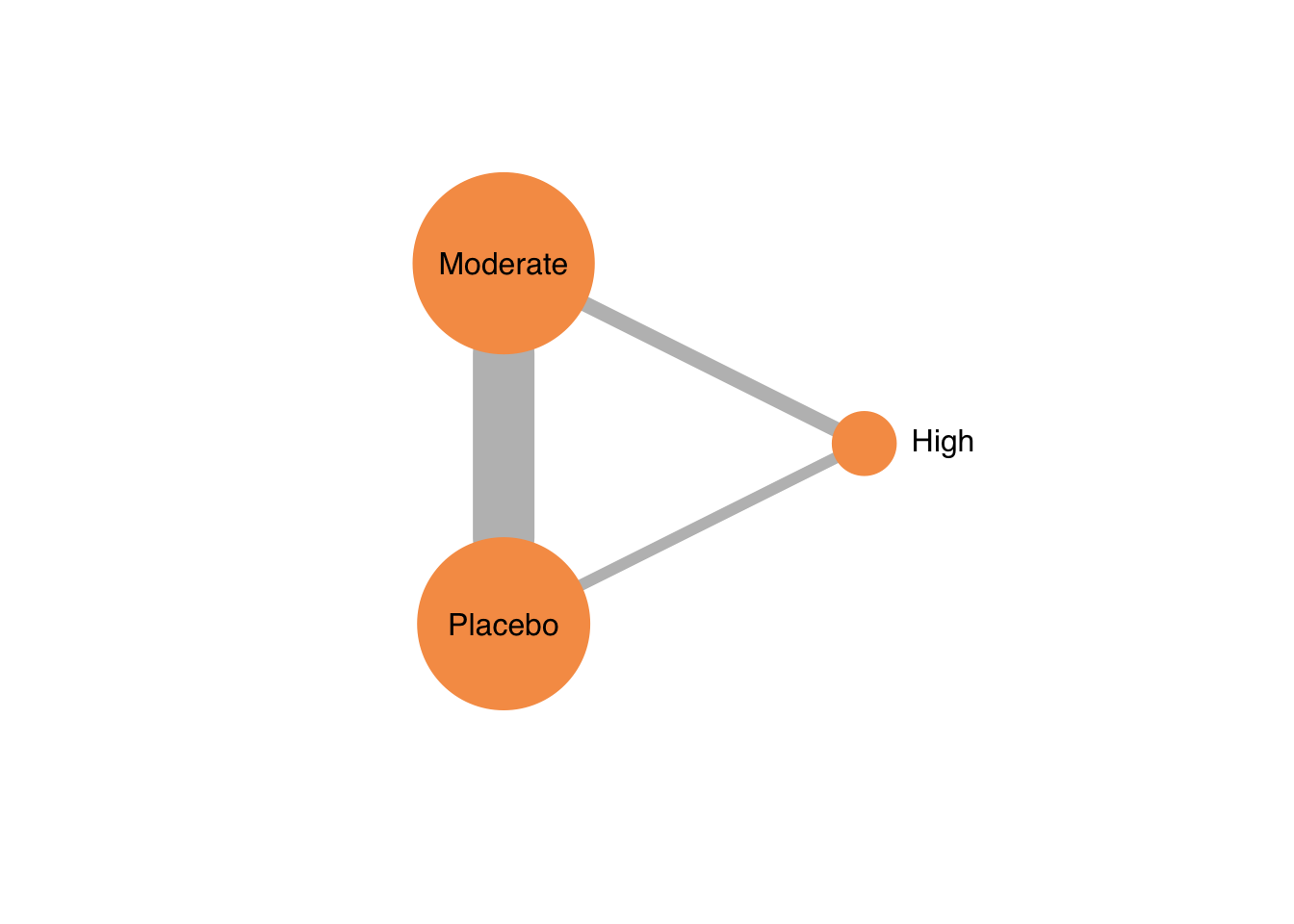
gemtcDavis <- mtc.network(data.ab=dfGemtc)

5.3.1 Network plot

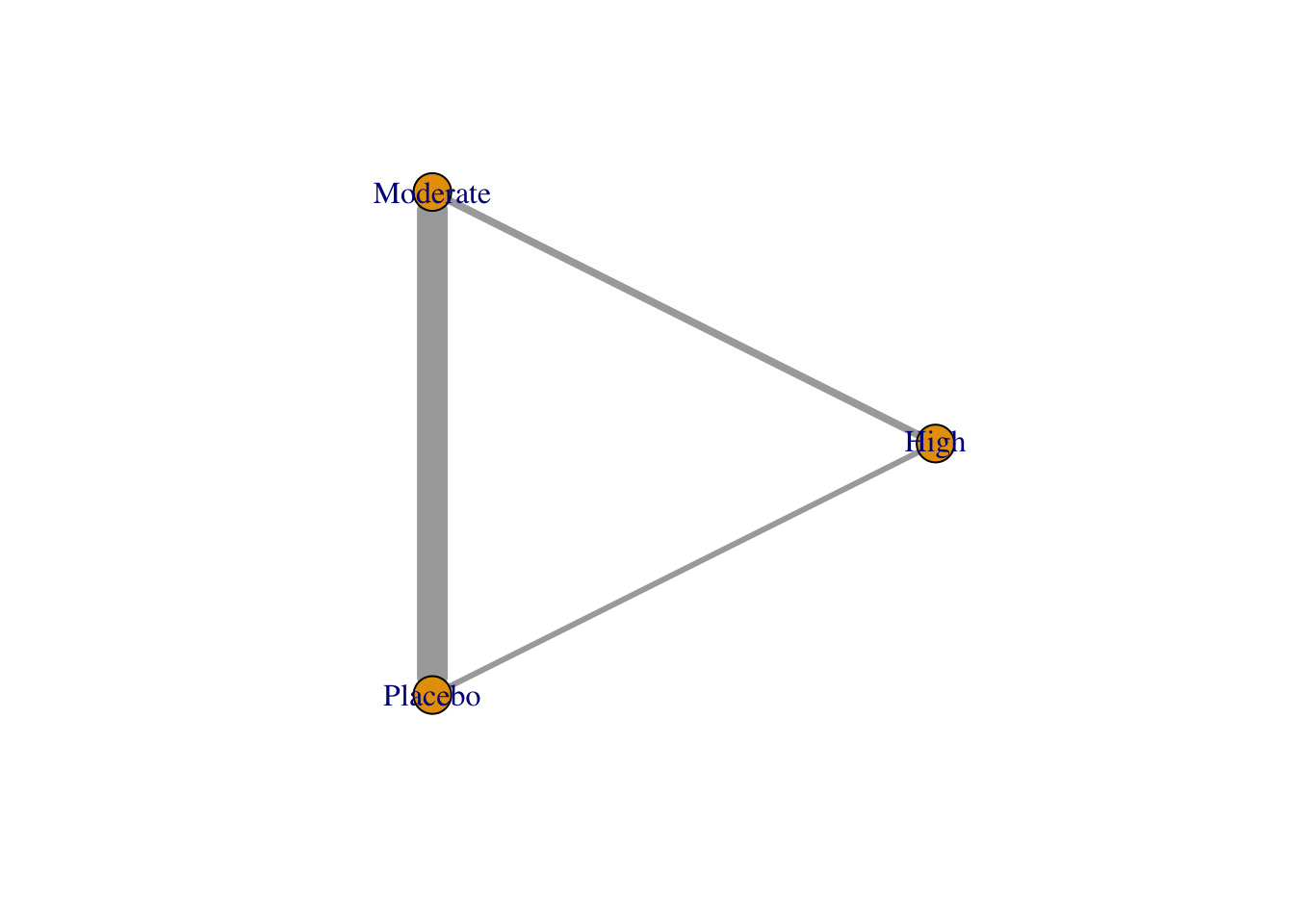
plot(gemtcDavis, use.description = TRUE)

use.description で description 列を参照するはずだが、どうも機能しない。

summary(gemtcDavis)
## $Description
## [1] "MTC dataset: Network"
## 
## $`Studies per treatment`
##     High Moderate  Placebo 
##        7       20       19 
## 
## $`Number of n-arm studies`
## 2-arm 
##    23 
## 
## $`Studies per treatment comparison`
##         t1       t2 nr
## 1     High Moderate  4
## 2     High  Placebo  3
## 3 Moderate  Placebo 16

5.3.2 モデル作成

mtcModelFixed <- mtc.model(gemtcDavis, linearModel="fixed", n.chain=4)
mtcModelRandom <- mtc.model(gemtcDavis, linearModel="random", n.chain=4)

5.3.3 モデル実行

mtcResFixed <- mtc.run(mtcModelFixed, n.adapt=5000, n.iter=10000, thin=10)
## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 46
##    Unobserved stochastic nodes: 25
##    Total graph size: 932
## 
## Initializing model
summary(mtcResFixed)
## 
## Results on the Log Odds Ratio scale
## 
## Iterations = 5010:15000
## Thinning interval = 10 
## Number of chains = 4 
## Sample size per chain = 1000 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##                     Mean      SD  Naive SE Time-series SE
## d.High.Moderate -0.05467 0.02648 0.0004187      0.0005180
## d.High.Placebo  -0.06094 0.02715 0.0004292      0.0005255
## 
## 2. Quantiles for each variable:
## 
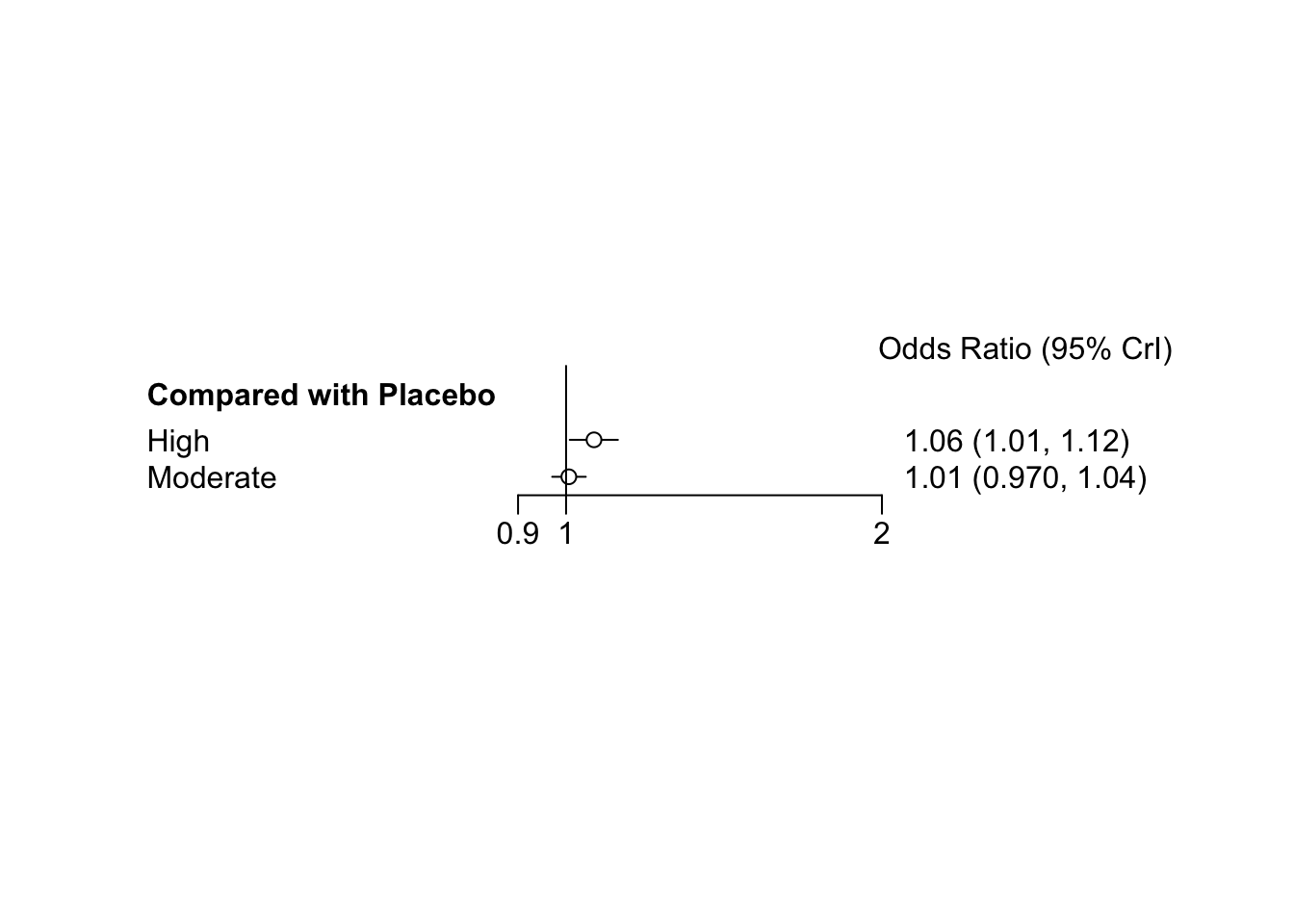
##                    2.5%      25%      50%      75%     97.5%
## d.High.Moderate -0.1063 -0.07213 -0.05463 -0.03698 -0.001840
## d.High.Placebo  -0.1137 -0.07938 -0.06128 -0.04247 -0.008131
## 
## -- Model fit (residual deviance):
## 
##     Dbar       pD      DIC 
## 49.80489 25.31706 75.12195 
## 
## 46 data points, ratio 1.083, I^2 = 10%
mtcResRandom <- mtc.run(mtcModelRandom, n.adapt=5000, n.iter=10000, thin=10)
## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 46
##    Unobserved stochastic nodes: 49
##    Total graph size: 990
## 
## Initializing model
summary(mtcResRandom)
## 
## Results on the Log Odds Ratio scale
## 
## Iterations = 5010:15000
## Thinning interval = 10 
## Number of chains = 4 
## Sample size per chain = 1000 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##                     Mean      SD  Naive SE Time-series SE
## d.High.Moderate -0.05219 0.03557 0.0005624       0.001384
## d.High.Placebo  -0.06220 0.03581 0.0005662       0.001535
## sd.d             0.03318 0.02706 0.0004279       0.001681
## 
## 2. Quantiles for each variable:
## 
##                       2.5%      25%      50%      75%    97.5%
## d.High.Moderate -0.1221050 -0.07454 -0.05168 -0.03040 0.019741
## d.High.Placebo  -0.1342510 -0.08623 -0.06020 -0.03937 0.007528
## sd.d             0.0003187  0.01243  0.02794  0.04823 0.095717
## 
## -- Model fit (residual deviance):
## 
##     Dbar       pD      DIC 
## 48.16189 27.98140 76.14329 
## 
## 46 data points, ratio 1.047, I^2 = 7%

5.3.4 収束の評価

plot(mtcResFixed)
plot(mtcResRandom)
library(coda)
gelman.plot(mtcResFixed)

gelman.plot(mtcResRandom)

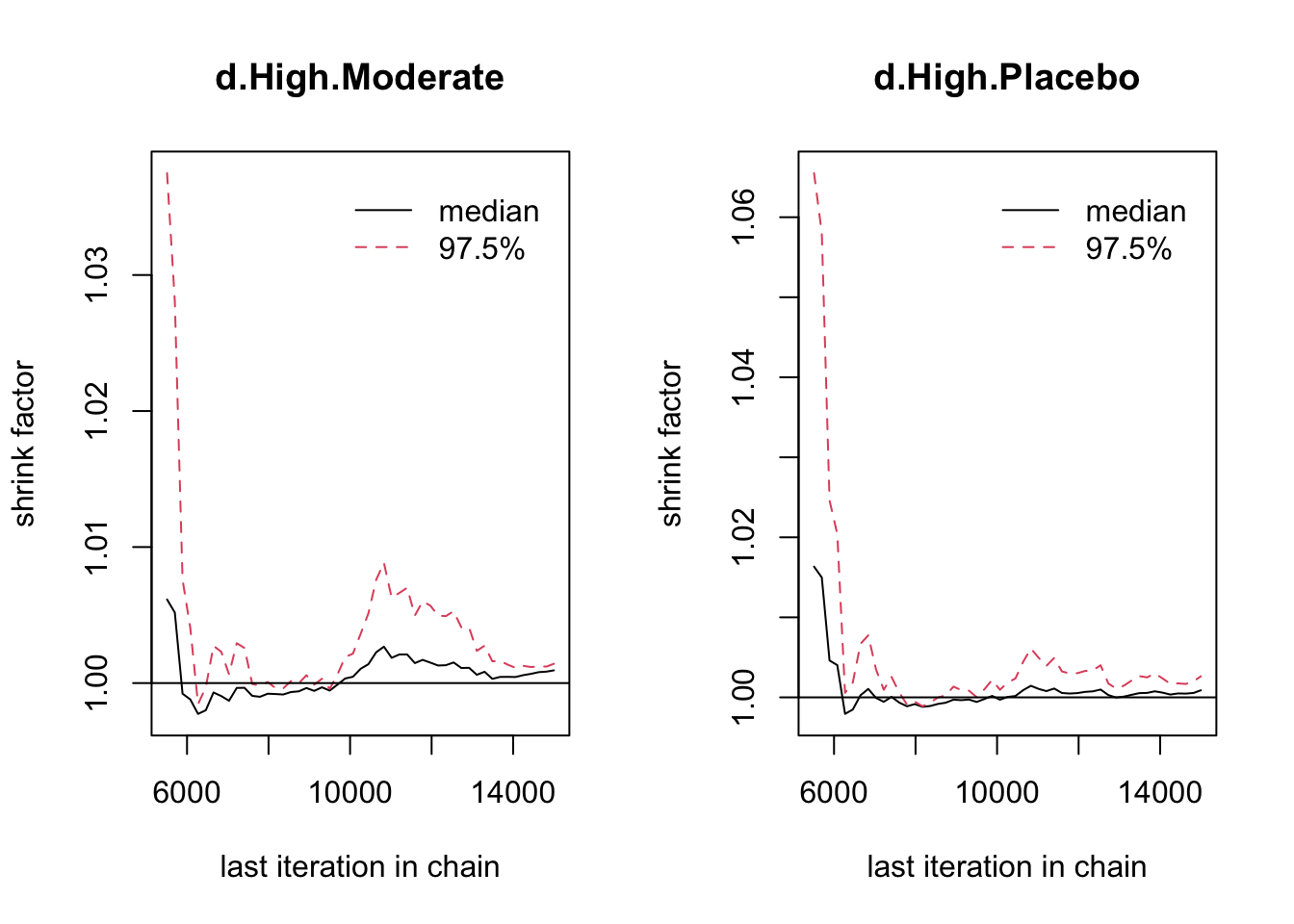
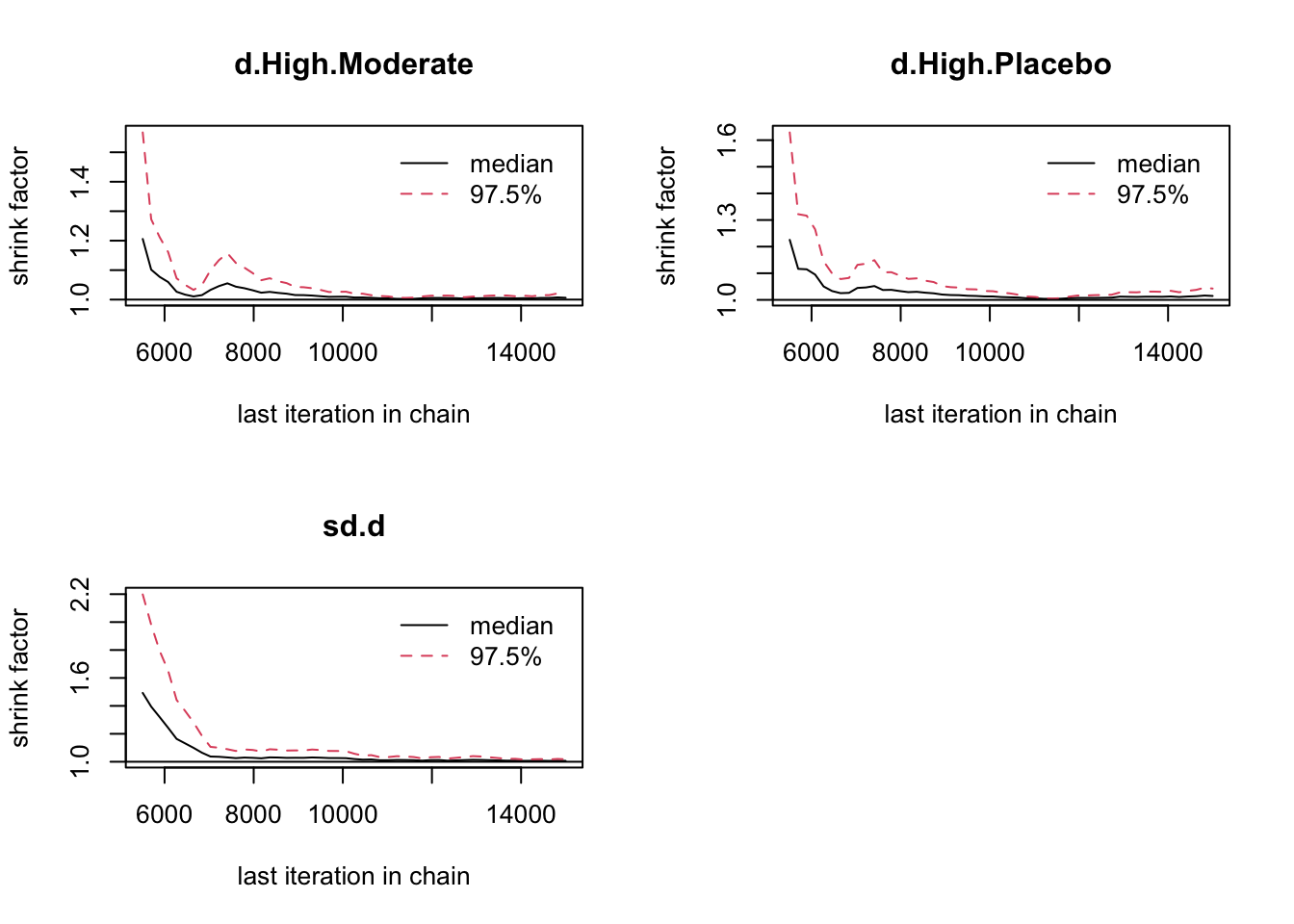
DIC は低い方が良い。Fixed が 74.75982、Random が75.98427。

gelman.diag(mtcResFixed)$mpsrf
## [1] 1.001424
gelman.diag(mtcResRandom)$mpsrf
## [1] 1.014965

1 に近い方が良い。

固定効果を採用。

5.3.5 適合度の評価

mtc.levplot(mtc.deviance(mtcResFixed))

5.3.6 一貫性の評価

エラーが出るため、検証中。

nodesplit <- mtc.nodesplit(gemtcDavis, 
                           linearModel = "random", 
                           likelihood = "normal",
                           link = "identity",
                           n.adapt = 5000, 
                           n.iter = 1e5, 
                           thin = 10)
plot(summary(nodesplit))

5.3.7 Ranking

rank <- rank.probability(mtcResFixed, preferredDirection=-1)
library(dmetar)
dmetar::sucra(rank, lower.is.better = TRUE)
##             SUCRA
## High     0.982625
## Moderate 0.327875
## Placebo  0.189500

5.3.8 Forest plot

gemtc::forest(relative.effect(mtcResFixed, t1="Placebo"), digits=3)

5.4 BUGSnet ベイジアン

BUGSnet では、arm-based データのみ対応している。

5.4.1 データ準備

BugsDavis <- data.prep(arm.data = dfArm,
                     varname.t = "treat",
                     varname.s = "Study")

5.4.2 Network plot

net.plot(BugsDavis,
         label.offset1 = c(6,0,0),
         node.scale = 5, 
         edge.scale=2)

label.offset1 で、外側にずらすことができる。順序は、High から反時計回り。

5.4.3 要約

TabBugsDavis <- net.tab(data = BugsDavis,
                        outcome = "X",
                        N = "Total", 
                        type.outcome = "binomial",
                        time = NULL)
TabBugsDavis$intervention
## # A tibble: 3 × 7
##   treat    n.studies n.events n.patients min.outcome max.outcome av.outcome
##   <chr>        <int>    <int>      <int>       <dbl>       <dbl>      <dbl>
## 1 High             7     4654      28126    0.0181         0.435      0.165
## 2 Moderate        20    10946      62682    0              0.621      0.175
## 3 Placebo         19     9661      60013    0.000316       0.597      0.161

5.4.4 モデル作成

BugsModelFixed <- nma.model(data=BugsDavis,
                     outcome="X",
                     N="Total",
                     reference="Placebo",
                     family="binomial",
                     link="log",
                     effects="fixed")

BugsModelRandom <- nma.model(data=BugsDavis,
                     outcome="X",
                     N="Total",
                     reference="Placebo",
                     family="binomial",
                     link="log",
                     effects="random")

5.4.5 モデル実行

n.adapt、n.inter、thin を色々試して、DIC 値を下げる。

set.seed(20190829)
BugsResFixed <- nma.run(BugsModelFixed,
                        n.adapt=5000,
                        n.iter=20000,
                        thin = 10)
## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 46
##    Unobserved stochastic nodes: 25
##    Total graph size: 1003
## 
## Initializing model
BugsResRandom <- nma.run(BugsModelRandom,
                        n.adapt=5000,
                        n.iter=20000,
                        thin = 10)
## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 46
##    Unobserved stochastic nodes: 49
##    Total graph size: 1040
## 
## Initializing model

5.4.6 収束の評価

nma.diag(BugsResFixed)

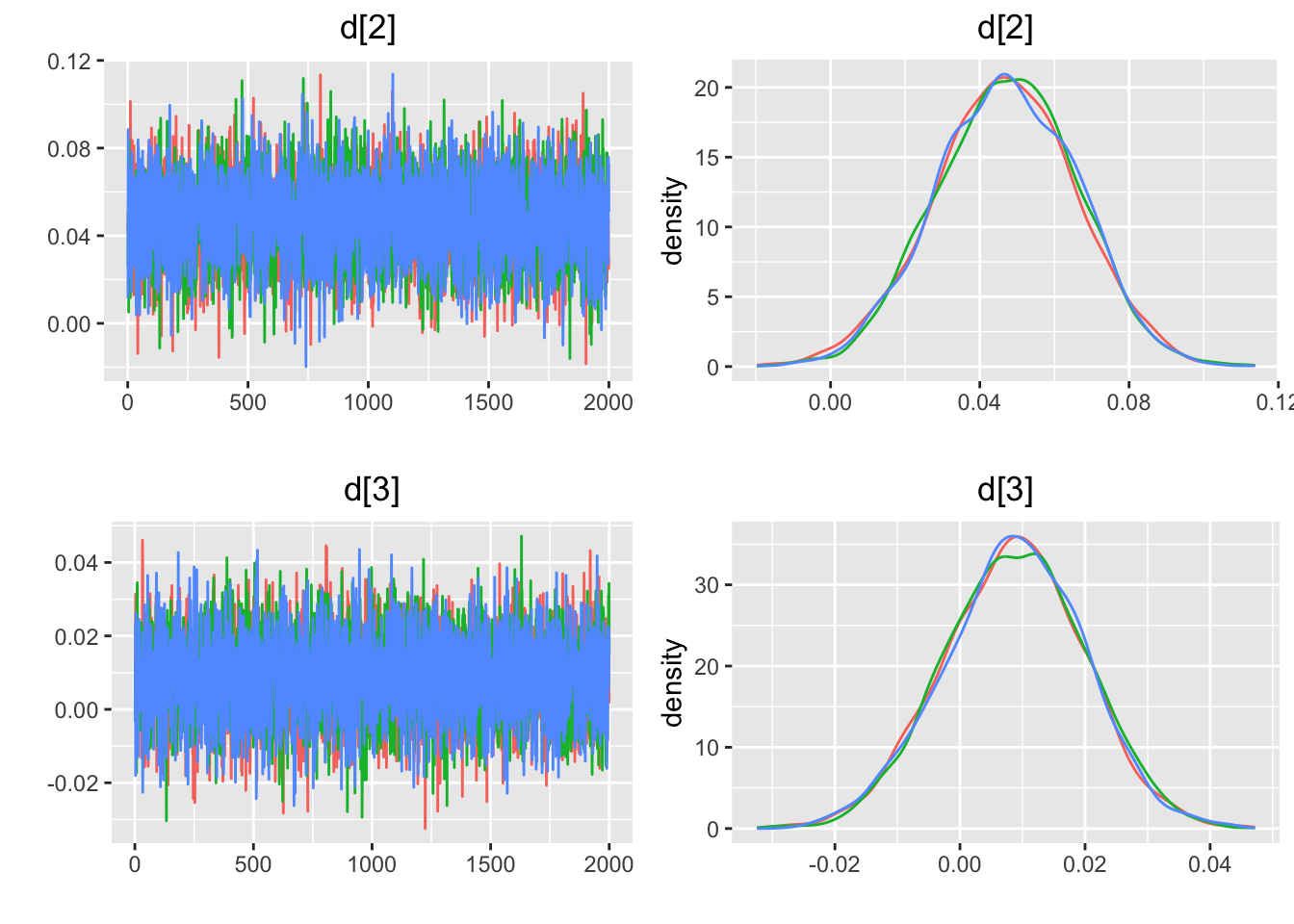
## $gelman.rubin
## $psrf
##      Point est. Upper C.I.
## d[2]   1.000028   1.000726
## d[3]   1.000239   1.001535
## 
## $mpsrf
## [1] 1.00032
## 
## attr(,"class")
## [1] "gelman.rubin.results"
## 
## $geweke
## $stats
##         Chain 1    Chain 2    Chain 3
## d[2] -1.0241199 0.29017330  1.2089093
## d[3]  0.5759415 0.06487731 -0.2986586
## 
## $frac1
## [1] 0.1
## 
## $frac2
## [1] 0.5
## 
## attr(,"class")
## [1] "geweke.results"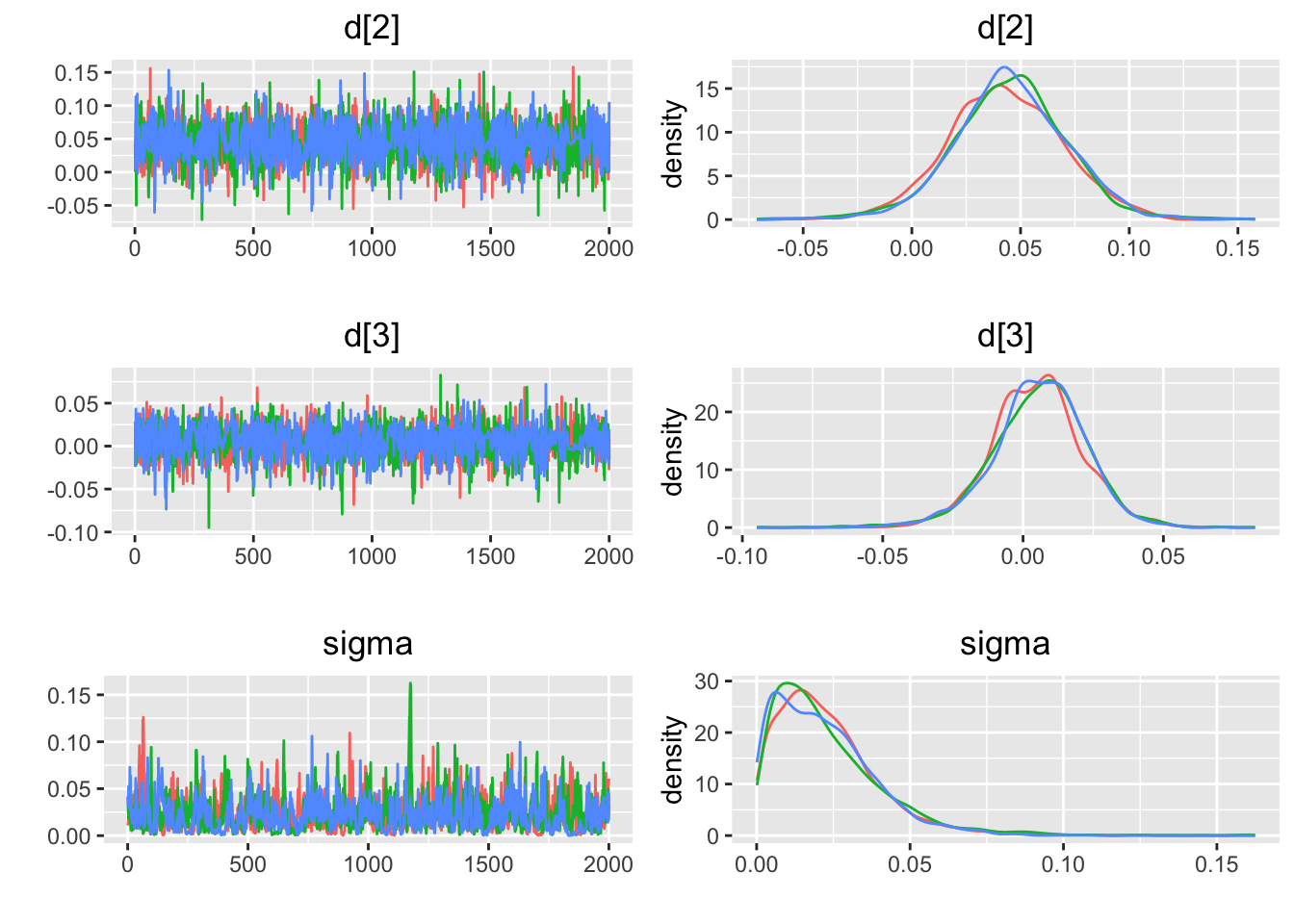
nma.diag(BugsResRandom)

## $gelman.rubin
## $psrf
##       Point est. Upper C.I.
## d[2]    1.001451   1.005226
## d[3]    1.002416   1.003517
## sigma   1.015574   1.025485
## 
## $mpsrf
## [1] 1.003493
## 
## attr(,"class")
## [1] "gelman.rubin.results"
## 
## $geweke
## $stats
##         Chain 1    Chain 2     Chain 3
## d[2]  0.1837099  0.5771300 -0.23362377
## d[3]  0.0948172  0.2085824 -0.04648464
## sigma 1.0791718 -1.4359398  1.50291837
## 
## $frac1
## [1] 0.1
## 
## $frac2
## [1] 0.5
## 
## attr(,"class")
## [1] "geweke.results"

5.4.7 適合度の評価

par(mfrow = c(1,2))
nma.fit(BugsResFixed, main = "Fixed Effects Model" )
## $DIC
## [1] NaN
## 
## $Dres
## [1] 48.59683
## 
## $pD
## [1] NaN
## 
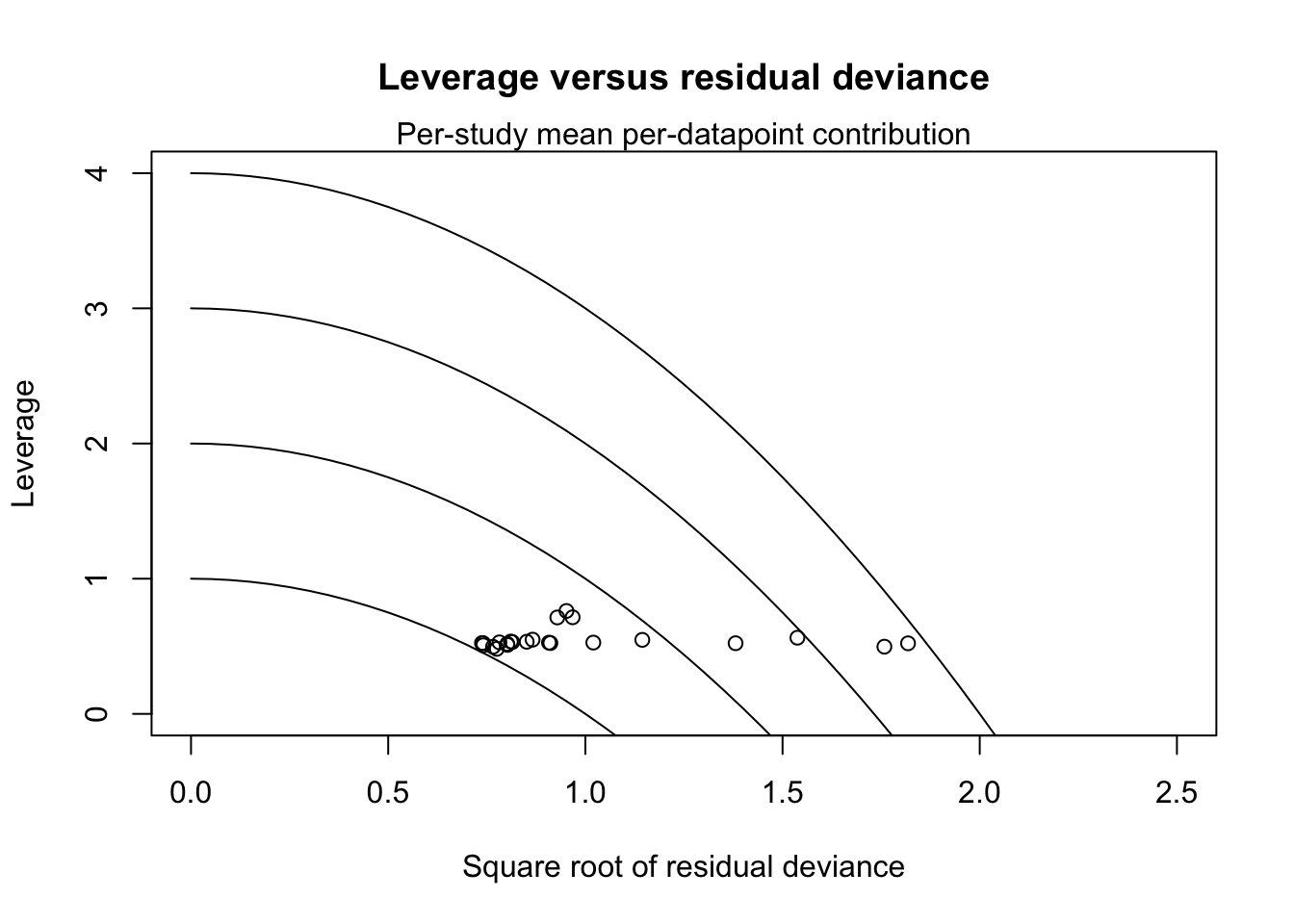
## $leverage
##                                                                                
## 1 0.3917105 0.5135493 0.6601816 0.527994 0.492735 0.3446973 0.5229203 0.5080603
##                                                                        
## 1 0.8223124 0.4955778 0.4653912 0.2130651 0.6613483 0.6453603 0.5338967
##                                                                        
## 1 0.4641055 0.5692151 0.8257768 0.5357165 0.5269379 0.5421835 0.4982472
##                                                                        
## 1 0.5087306 0.5463266 0.4273331 0.6578787 0.5226709 0.5246775 0.6440997
##                                                                            
## 1 0.4951171 0.5216668 NaN 0.5356726 0.5094069 0.6381509 0.6488496 0.6697803
##                                                                        
## 1 0.4277221 0.5215553 0.4595749 0.8355391 0.4891002 0.5389909 0.5269903
##                      
## 1 0.5581556 0.4851809
## 
## $w
##     r.1.1.     r.2.1.     r.3.1.     r.4.1.     r.5.1.     r.6.1.     r.7.1. 
## -0.8890095  0.7864045 -1.3762191  0.7603438 -0.7930587 -1.8690288  1.3981543 
##     r.8.1.     r.9.1.    r.10.1.    r.11.1.    r.12.1.    r.13.1.    r.14.1. 
##  0.7926714  1.2791974 -0.9077386 -0.7488842 -1.1608474  1.0287761  0.8554874 
##    r.15.1.    r.16.1.    r.17.1.    r.18.1.    r.19.1.    r.20.1.    r.21.1. 
##  0.7506298 -0.8002997  0.9308799  0.9190619  1.0548751 -0.8289113 -0.7389336 
##    r.22.1.    r.23.1.     r.1.2.     r.2.2.     r.3.2.     r.4.2.     r.5.2. 
## -0.8379113  0.7616019  0.7730933 -0.8218558  1.3868740 -0.7631022  0.7872248 
##     r.6.2.     r.7.2.     r.8.2.     r.9.2.    r.10.2.    r.11.2.    r.12.2. 
##  1.6299092 -1.4233002 -0.8048225 -2.2256995  0.8695228  0.7187657  0.8548239 
##    r.13.2.    r.14.2.    r.15.2.    r.16.2.    r.17.2.    r.18.2.    r.19.2. 
## -1.0239312 -0.8743759 -0.8375506  0.7683183 -0.9571942 -0.9272453 -1.1105402 
##    r.20.2.    r.21.2.    r.22.2.    r.23.2. 
##  0.8256853  0.7273149  0.8275154 -0.7829415 
## 
## $pmdev
##  dev_a.1.1.  dev_a.2.1.  dev_a.3.1.  dev_a.4.1.  dev_a.5.1.  dev_a.6.1. 
##   0.7903378   0.6184321   1.8939791   0.5781227   0.6289420   3.4932687 
##  dev_a.7.1.  dev_a.8.1.  dev_a.9.1. dev_a.10.1. dev_a.11.1. dev_a.12.1. 
##   1.9548356   0.6283280   1.6363460   0.8239894   0.5608275   1.3475667 
## dev_a.13.1. dev_a.14.1. dev_a.15.1. dev_a.16.1. dev_a.17.1. dev_a.18.1. 
##   1.0583803   0.7318587   0.5634450   0.6404796   0.8665374   0.8446748 
## dev_a.19.1. dev_a.20.1. dev_a.21.1. dev_a.22.1. dev_a.23.1.  dev_a.1.2. 
##   1.1127615   0.6870940   0.5460228   0.7020953   0.5800374   0.5976733 
##  dev_a.2.2.  dev_a.3.2.  dev_a.4.2.  dev_a.5.2.  dev_a.6.2.  dev_a.7.2. 
##   0.6754470   1.9234195   0.5823250   0.6197228   2.6566040   2.0257834 
##  dev_a.8.2.  dev_a.9.2. dev_a.10.2. dev_a.11.2. dev_a.12.2. dev_a.13.2. 
##   0.6477392   4.9537381   0.7560700   0.5166242   0.7307239   1.0484352 
## dev_a.14.2. dev_a.15.2. dev_a.16.2. dev_a.17.2. dev_a.18.2. dev_a.19.2. 
##   0.7645332   0.7014910   0.5903130   0.9162207   0.8597838   1.2332995 
## dev_a.20.2. dev_a.21.2. dev_a.22.2. dev_a.23.2. 
##   0.6817562   0.5289870   0.6847817   0.6129975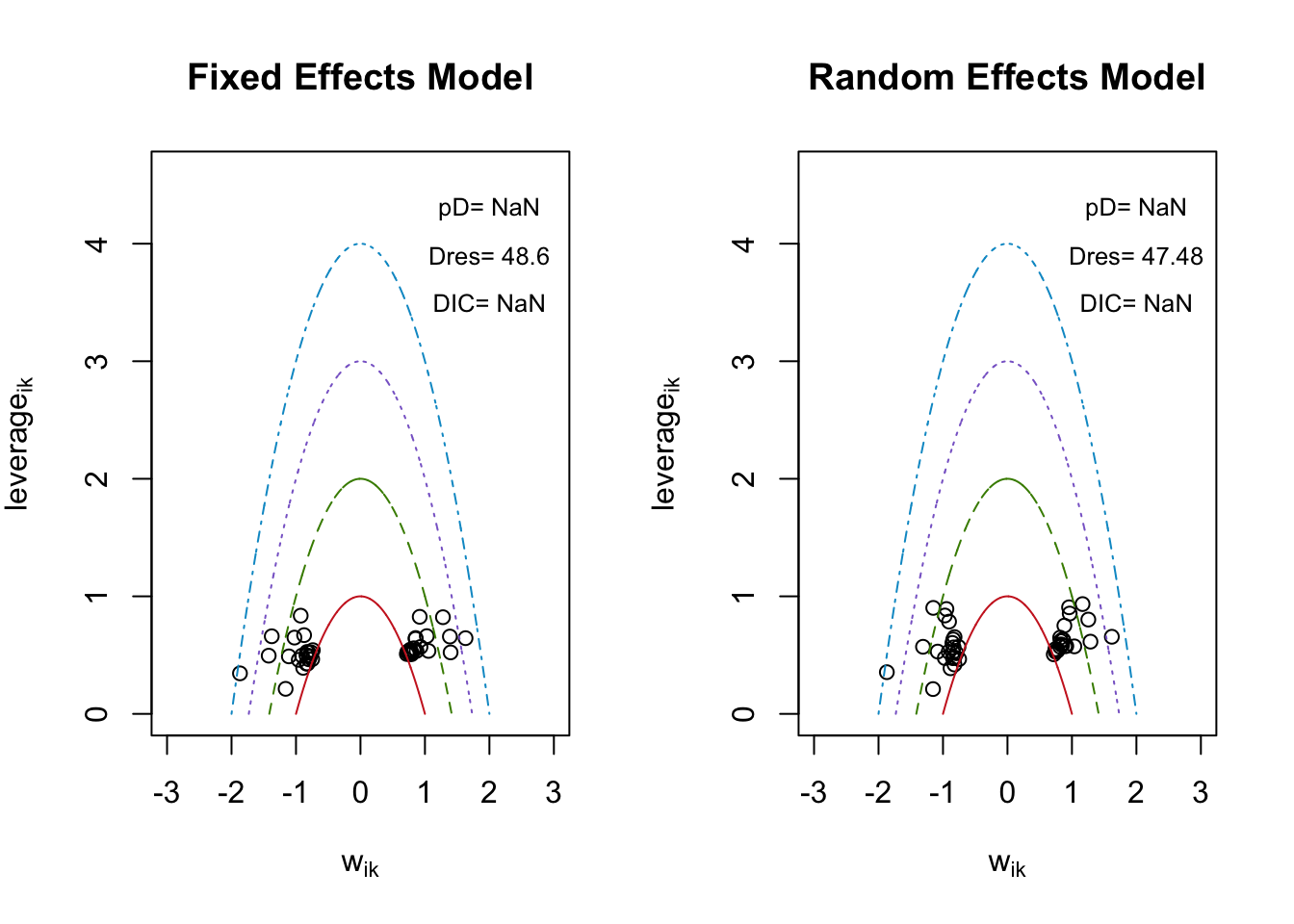
nma.fit(BugsResRandom, main= "Random Effects Model")

## $DIC
## [1] NaN
## 
## $Dres
## [1] 47.48206
## 
## $pD
## [1] NaN
## 
## $leverage
##                                                                        
## 1 0.3879883 0.5709878 0.9016669 0.6484318 0.5657538 0.3547065 0.6144591
##                                                                        
## 1 0.6193026 0.8022221 0.5282019 0.4659938 0.2109391 0.8535578 0.7508483
##                                                                        
## 1 0.5286571 0.4804632 0.5770053 0.9066433 0.5742166 0.6035965 0.5697343
##                                                                       
## 1 0.524471 0.5421301 0.5434343 0.4736803 0.9340473 0.6531751 0.5910543
##                                                                            
## 1 0.6560415 0.5707983 0.6331449 NaN 0.5766273 0.5064597 0.6329557 0.8369056
##                                                                                
## 1 0.7850472 0.4198679 0.5365641 0.475001 0.8921608 0.5299677 0.627478 0.5505375
##                      
## 1 0.5854012 0.5160237
## 
## $w
##     r.1.1.     r.2.1.     r.3.1.     r.4.1.     r.5.1.     r.6.1.     r.7.1. 
## -0.8830170  0.8182676 -1.1513447  0.8168469 -0.8351248 -1.8710162  1.2872817 
##     r.8.1.     r.9.1.    r.10.1.    r.11.1.    r.12.1.    r.13.1.    r.14.1. 
##  0.8242121  1.2539918 -0.9121564 -0.7497071 -1.1549073  0.9652171  0.8827545 
##    r.15.1.    r.16.1.    r.17.1.    r.18.1.    r.19.1.    r.20.1.    r.21.1. 
##  0.7474218 -0.8226919  0.9125323  0.9552475  1.0375318 -0.8545726 -0.7591116 
##    r.22.1.    r.23.1.     r.1.2.     r.2.2.     r.3.2.     r.4.2.     r.5.2. 
## -0.8463772  0.7701794  0.7752967 -0.8465064  1.1645561 -0.8205691  0.8295536 
##     r.6.2.     r.7.2.     r.8.2.     r.9.2.    r.10.2.    r.11.2.    r.12.2. 
##  1.6189623 -1.3101292 -0.8409299 -2.2355998  0.8914944  0.7180637  0.8557594 
##    r.13.2.    r.14.2.    r.15.2.    r.16.2.    r.17.2.    r.18.2.    r.19.2. 
## -0.9704043 -0.9060763 -0.8220410  0.7733053 -0.9718819 -0.9468681 -1.0821366 
##    r.20.2.    r.21.2.    r.22.2.    r.23.2. 
##  0.8663692  0.7426384  0.8488024 -0.7932010 
## 
## $pmdev
##  dev_a.1.1.  dev_a.2.1.  dev_a.3.1.  dev_a.4.1.  dev_a.5.1.  dev_a.6.1. 
##   0.7797191   0.6695619   1.3255947   0.6672389   0.6974334   3.5007017 
##  dev_a.7.1.  dev_a.8.1.  dev_a.9.1. dev_a.10.1. dev_a.11.1. dev_a.12.1. 
##   1.6570941   0.6793256   1.5724954   0.8320293   0.5620608   1.3338109 
## dev_a.13.1. dev_a.14.1. dev_a.15.1. dev_a.16.1. dev_a.17.1. dev_a.18.1. 
##   0.9316440   0.7792556   0.5586393   0.6768220   0.8327152   0.9124977 
## dev_a.19.1. dev_a.20.1. dev_a.21.1. dev_a.22.1. dev_a.23.1.  dev_a.1.2. 
##   1.0764723   0.7302943   0.5762504   0.7163544   0.5931762   0.6010850 
##  dev_a.2.2.  dev_a.3.2.  dev_a.4.2.  dev_a.5.2.  dev_a.6.2.  dev_a.7.2. 
##   0.7165730   1.3561909   0.6733336   0.6881592   2.6210390   1.7164384 
##  dev_a.8.2.  dev_a.9.2. dev_a.10.2. dev_a.11.2. dev_a.12.2. dev_a.13.2. 
##   0.7071631   4.9979063   0.7947623   0.5156155   0.7323241   0.9416846 
## dev_a.14.2. dev_a.15.2. dev_a.16.2. dev_a.17.2. dev_a.18.2. dev_a.19.2. 
##   0.8209742   0.6757514   0.5980010   0.9445543   0.8965593   1.1710196 
## dev_a.20.2. dev_a.21.2. dev_a.22.2. dev_a.23.2. 
##   0.7505955   0.5515119   0.7204655   0.6291679

sD/DIC が計算されない。調査中。

5.4.8 一貫性の評価

固定効果のヒートプロットを作成する。

bugsLeague <- nma.league(BugsResFixed,  
                         central.tdcy="median")
bugsLeague$heatplot

Scura plot 後に order = bugsSucra$order とすると、順序が一致する。

5.4.9 Ranking

bugsSucra <- nma.rank(BugsResFixed, largerbetter=FALSE, sucra.palette= "Set1")
bugsSucra$sucraplot

5.4.10 Forest plot

nma.forest(BugsResFixed,
           comparator = "Placebo")

References

Davis, John W, and Susan C Weller. 2021. “Intensity of Statin Therapy and Muscle Symptoms: A Network Meta-Analysis of 153 000 Patients.” BMJ Open 11 (6): e043714.