Chapter 3 Standaridised Mean Difference
3.1 はじめに
Ruff et al. (2022) は、齲蝕に対する治療法が口腔の健康関連の生活の質 (OHRQoL)に与える影響を調査したネットワークメタ分析である。19件の研究を含み、SDF, ART, FV といった治療方法と、Placebo と齲蝕なしの５群がある。主要アウトカムは ECOHIS という QOL 評価。これは0〜52点で、低い方が良い。
- SDF: silver diamine fluoride
- ART: atraumatic restorative tretments
- FV: fluoride varnish
データを読み込む。データのうち、３行目と９行目は解析に用いないため、すぐに削除する。
3.1.1 meta 頻度論的ペアワイズメタ
パッケージは{meta}を使う。
SMD は連続数値であるため、用いる関数は metacont() となる。
meta*() 関数は、基本的に２群の比較のデータテーブルを用いる。
３群（A, B, C）比較の場合は、対照群Cに対してA-Cで1行、B-Cで1行とする。
また、studlab を同じにすることで、同一研究であることを表す。
この段階はまだペアワイズ分析。
library(meta)
metaRuff2022 <- metacont(n.e = Ne,
mean.e = Me,
sd.e = Se,
n.c = Nc,
mean.c = Mc,
sd.c = Sc,
studlab = studlab,
data = dfRuff2022[c(1,5,7,8,10),],
sm = "SMD",
fixed = FALSE,
label.e = "Experimental",
label.c = "Control",
prediction = TRUE)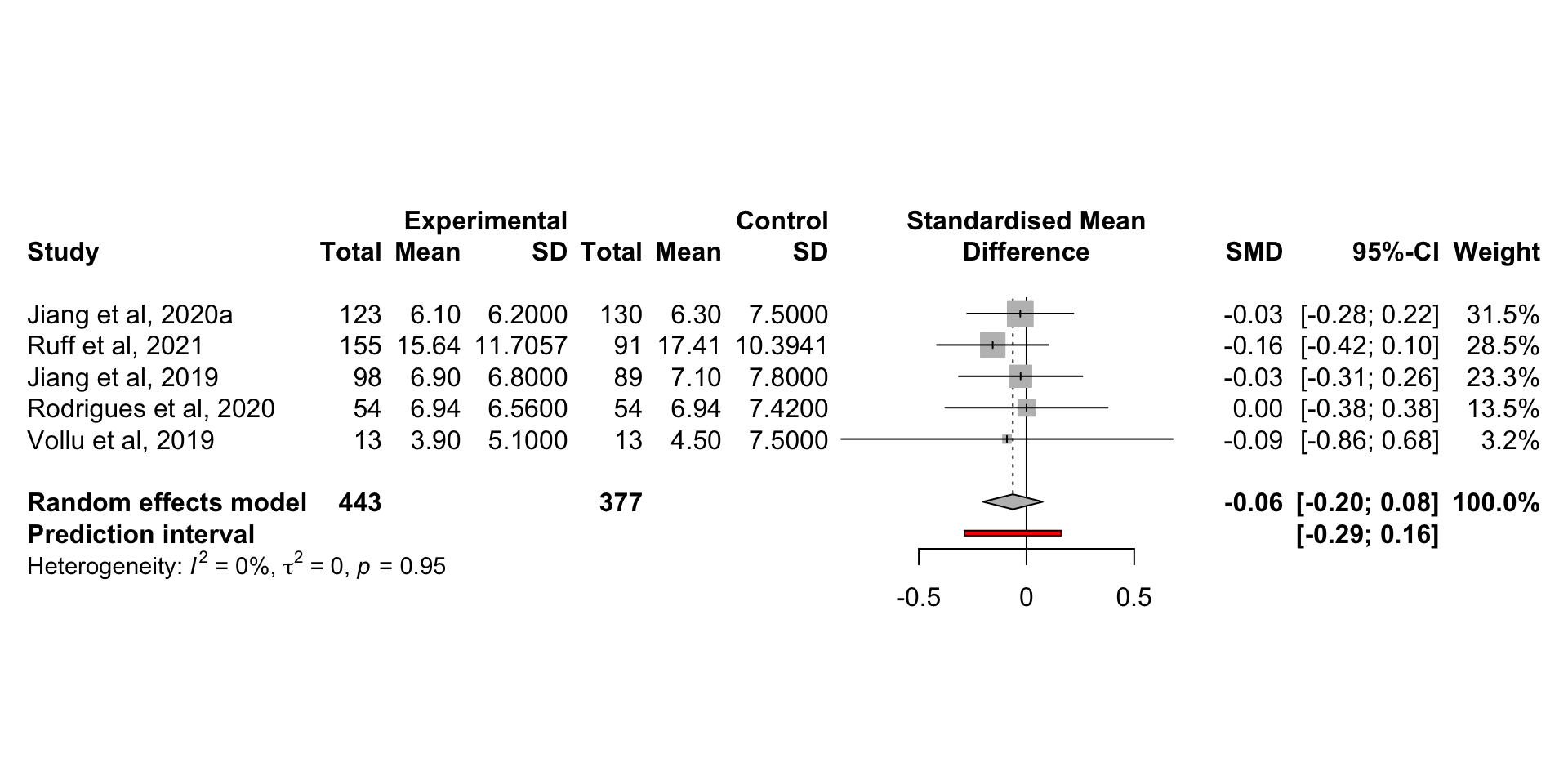
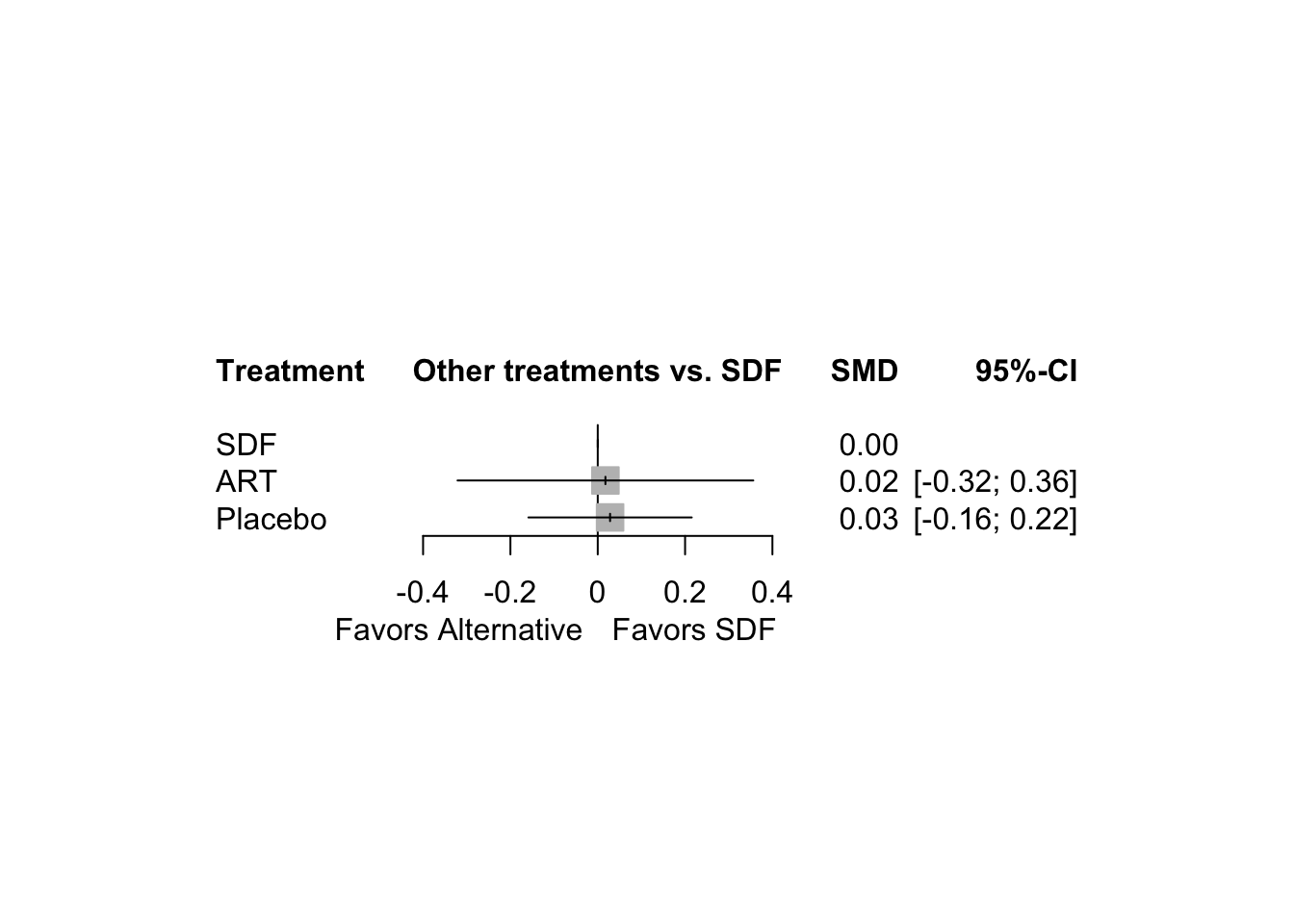
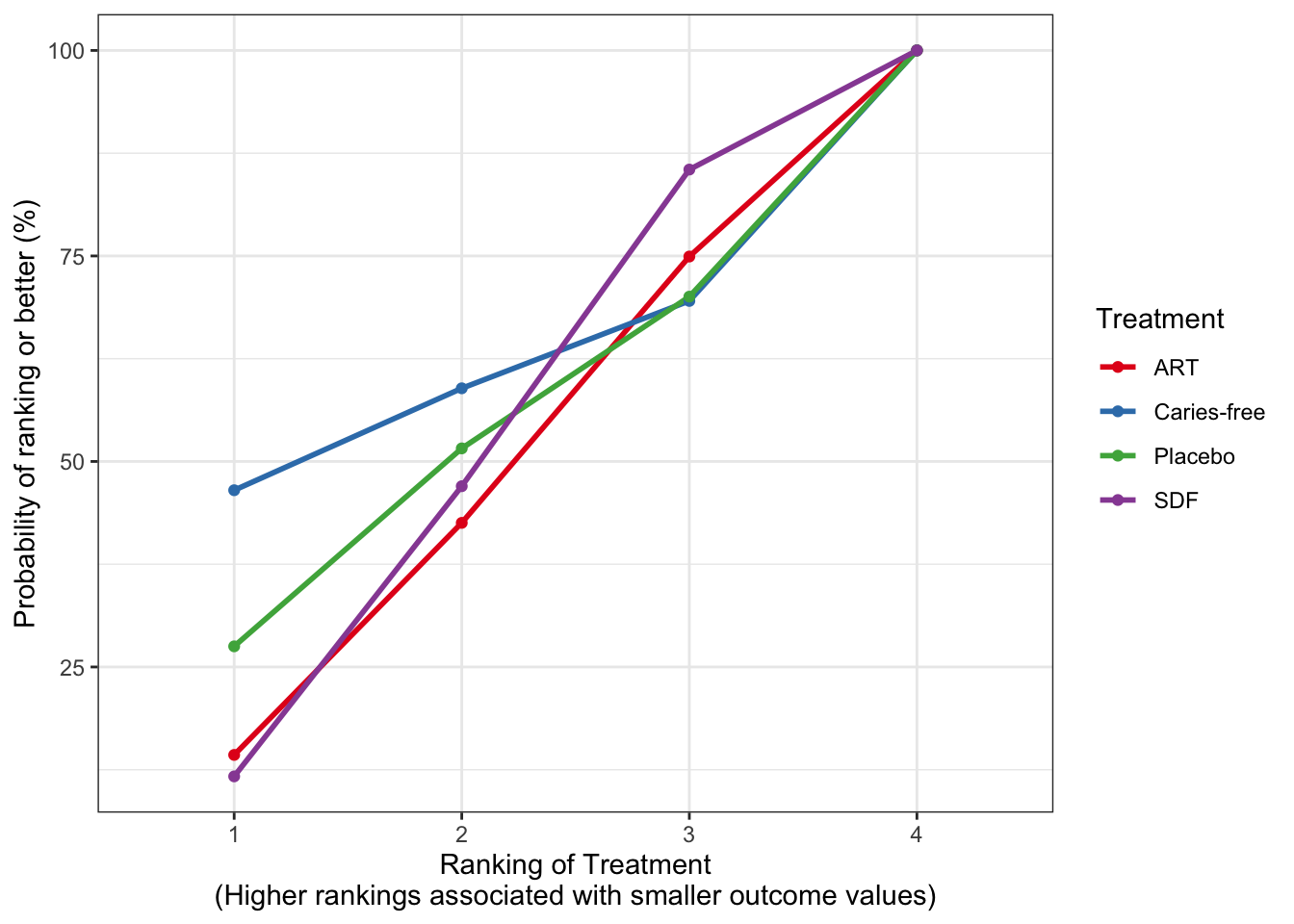
この図は、元論文の FIg. 2 と同じ。
3.2 netmeta 頻度論
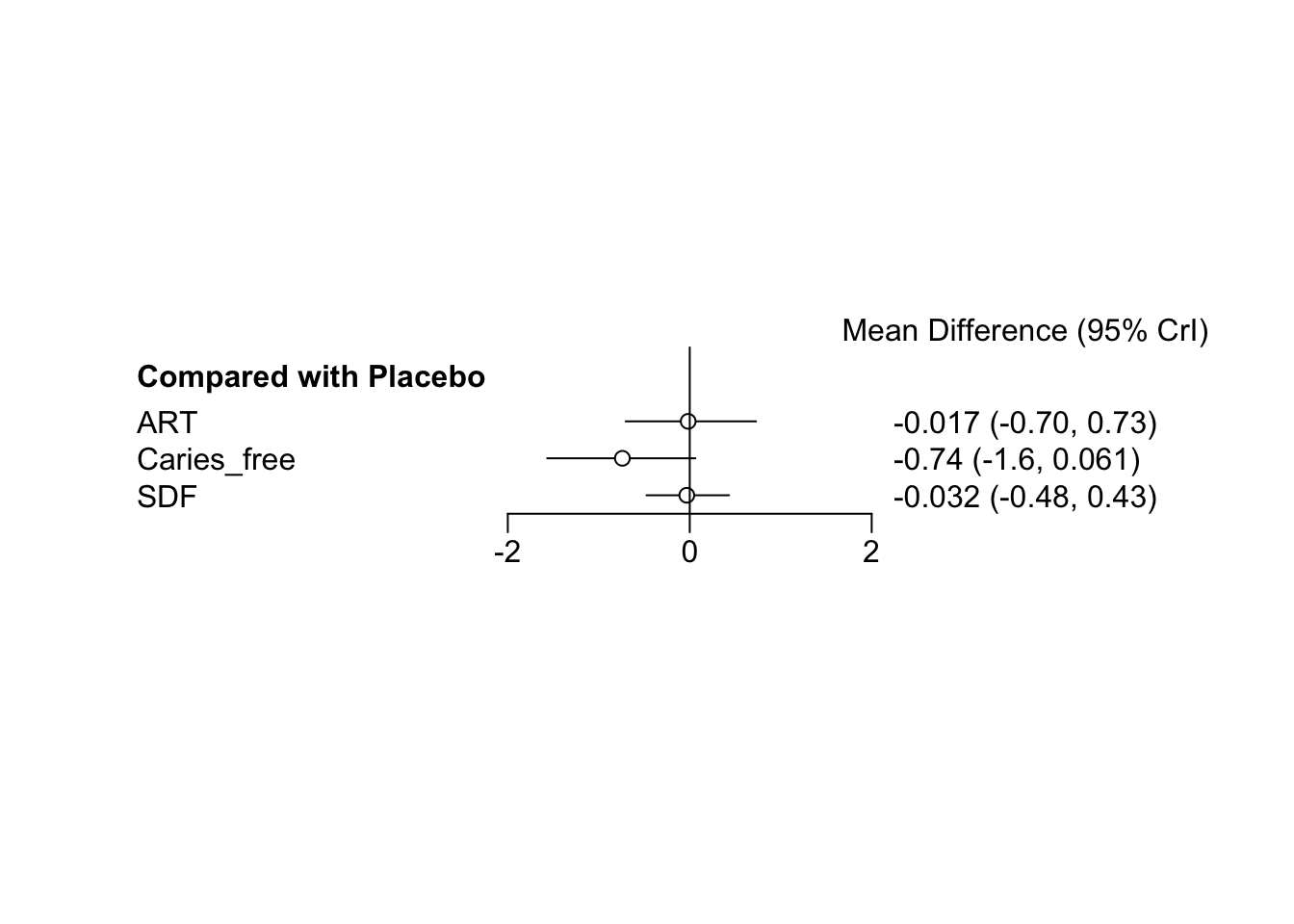
ここから、いよいよネットワーク分析になる。参照する治療方法は SDF。
library(netmeta)
netmetaRuff <- netmeta(TE = TE,
seTE = seTE,
treat1 = treat,
treat2 = control,
studlab = studlab,
data = dfRuff2022,
sm = "SMD",
fixed = TRUE,
random = FALSE,
reference.group = "SDF",
details.chkmultiarm = TRUE,
sep.trts = " vs ")## Comparison not considered in network meta-analysis:
## studlab treat1 treat2 TE seTE
## Jiang et al, 2020b SDF Caries-free NA NA3.2.1 要約
## Original data:
##
## treat1 treat2 TE seTE
## Jiang et al, 2020a Placebo SDF 0.0289 0.1258
## Jiang et al, 2019 Placebo SDF 0.0273 0.1464
## Rodrigues et al, 2020 ART SDF -0.0000 0.1925
## Vollu et al, 2019 ART SDF 0.0906 0.3925
##
## Number of treatment arms (by study):
## narms
## Jiang et al, 2020a 2
## Jiang et al, 2019 2
## Rodrigues et al, 2020 2
## Vollu et al, 2019 2
##
## Results (common effects model):
##
## treat1 treat2 SMD 95%-CI Q leverage
## Jiang et al, 2020a Placebo SDF 0.0282 [-0.1588; 0.2152] 0.00 0.58
## Jiang et al, 2019 Placebo SDF 0.0282 [-0.1588; 0.2152] 0.00 0.42
## Rodrigues et al, 2020 ART SDF 0.0176 [-0.3211; 0.3562] 0.01 0.81
## Vollu et al, 2019 ART SDF 0.0176 [-0.3211; 0.3562] 0.03 0.19
##
## Number of studies: k = 4
## Number of pairwise comparisons: m = 4
## Number of treatments: n = 3
## Number of designs: d = 2
##
## Common effects model
##
## Treatment estimate (sm = 'SMD', comparison: other treatments vs 'SDF'):
## SMD 95%-CI z p-value
## ART 0.0176 [-0.3211; 0.3562] 0.10 0.9190
## Placebo 0.0282 [-0.1588; 0.2152] 0.30 0.7674
## SDF . . . .
##
## Quantifying heterogeneity / inconsistency:
## tau^2 = 0; tau = 0; I^2 = 0% [0.0%; 89.6%]
##
## Tests of heterogeneity (within designs) and inconsistency (between designs):
## Q d.f. p-value
## Total 0.04 2 0.9787
## Within designs 0.04 2 0.9787
## Between designs 0.00 0 --3.2.2 Network plot
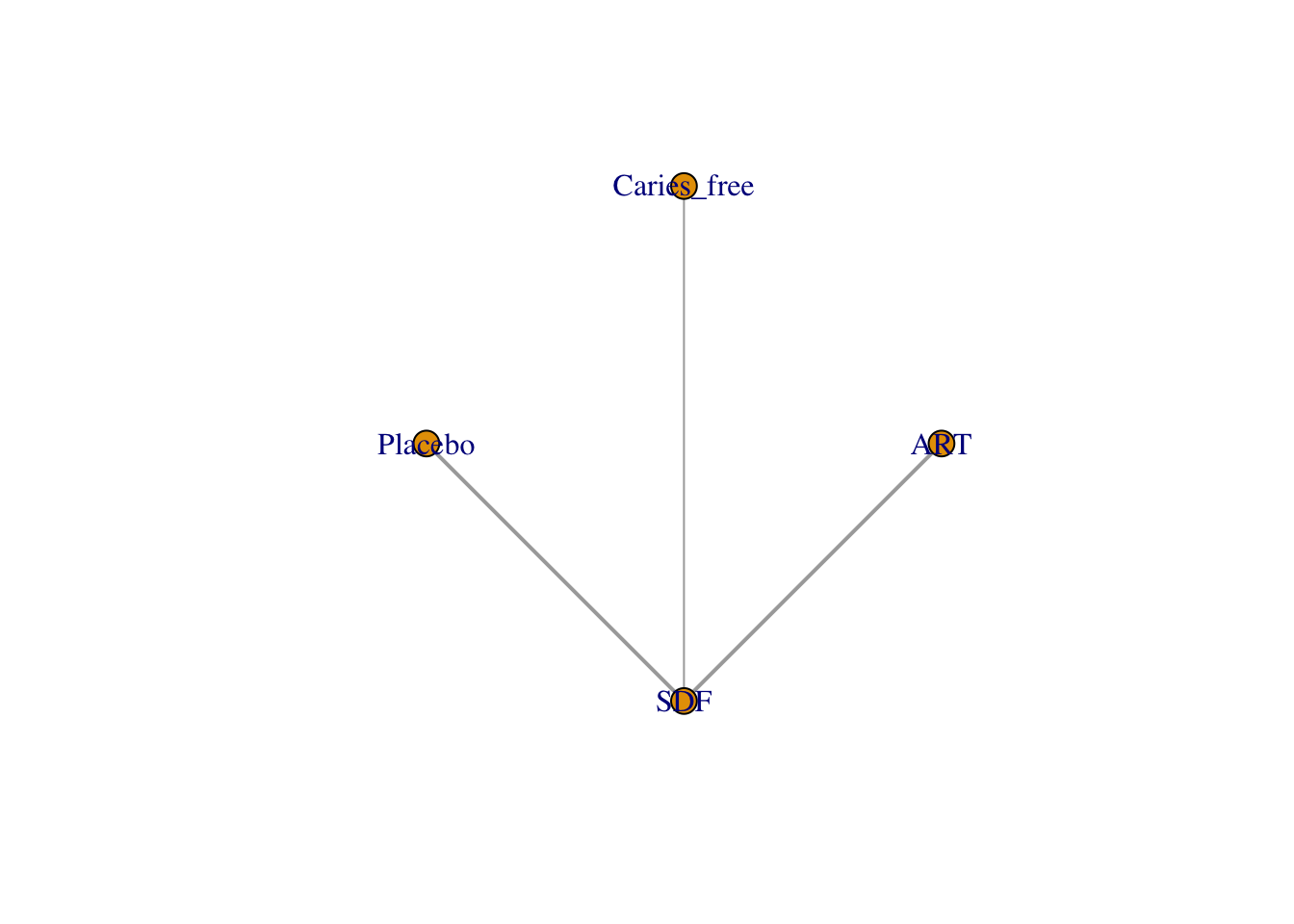
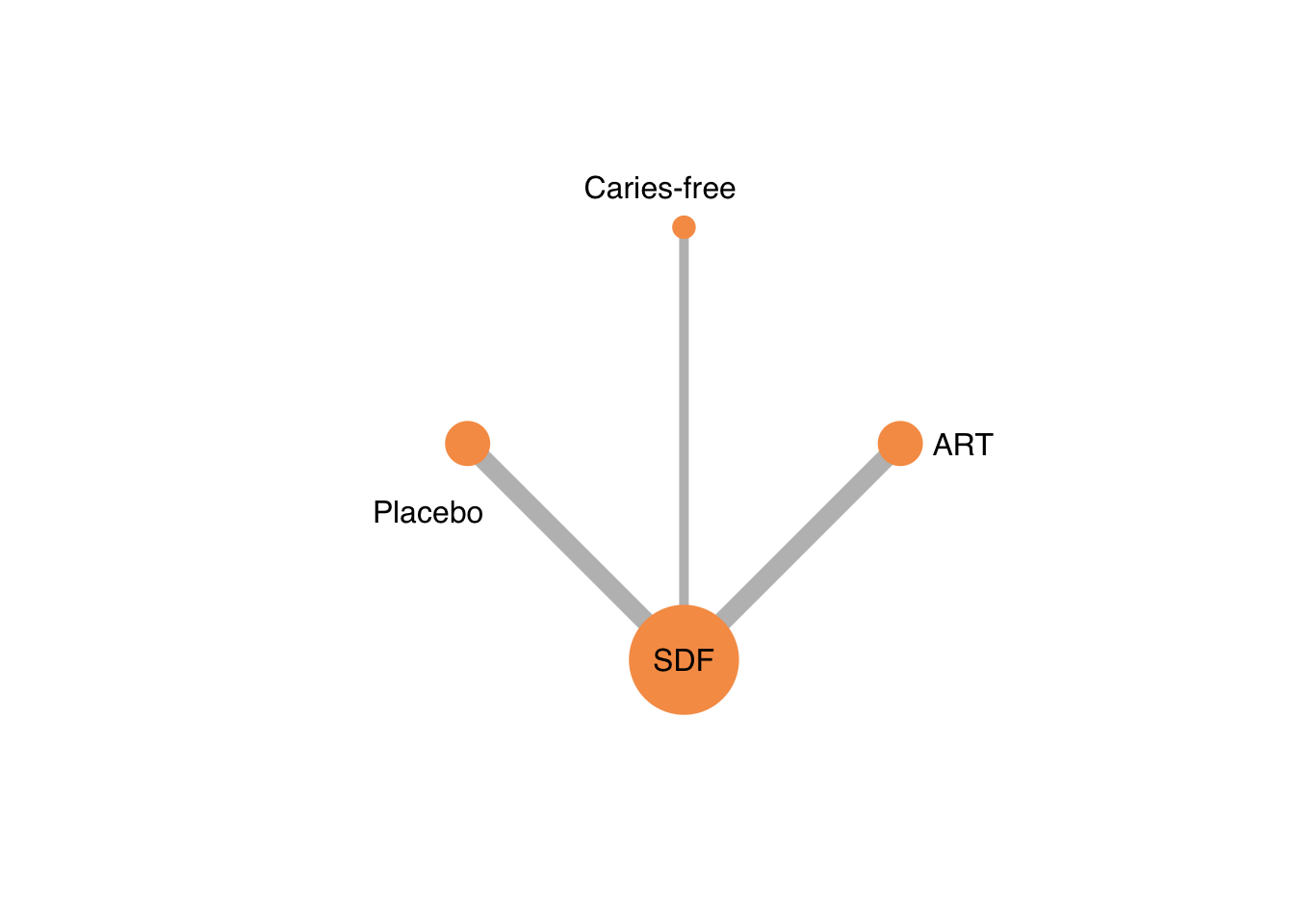
グラフを描く。
netgraph(netmetaRuff,
bg.points = "white",
plastic = FALSE, # 3Dではなくする
points = TRUE, # ノードを表示する
thickness = "number.of.studies", # 線の太さを研究数にする
multiarm = TRUE)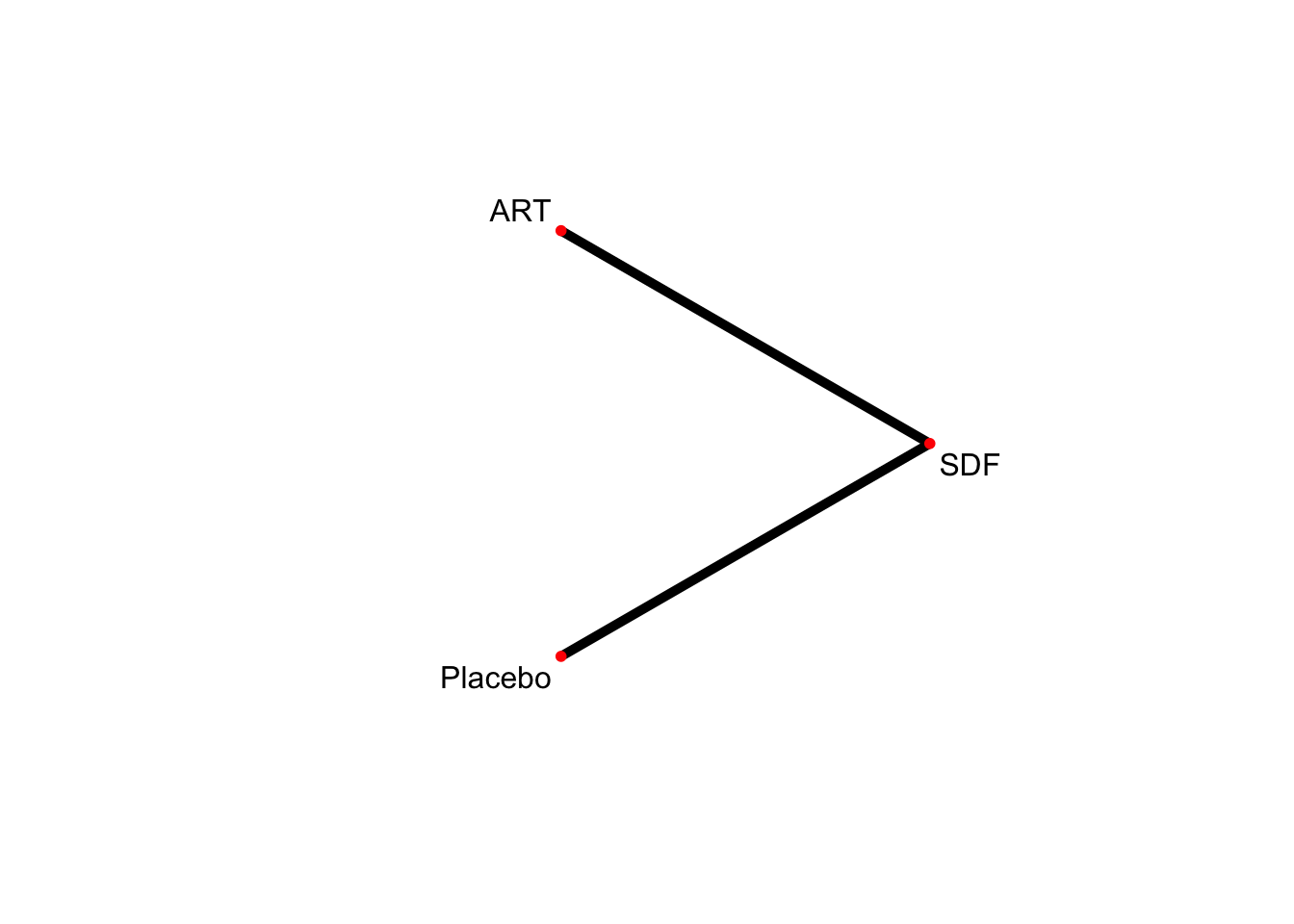
3.2.3 一貫性の評価
## Q statistics to assess homogeneity / consistency
##
## Q df p-value
## Total 0.04 2 0.9787
## Within designs 0.04 2 0.9787
## Between designs 0.00 0 --
##
## Design-specific decomposition of within-designs Q statistic
##
## Design Q df p-value
## SDF vs ART 0.04 1 0.8358
## SDF vs Placebo 0.00 1 0.9934
##
## Q statistic to assess consistency under the assumption of
## a full design-by-treatment interaction random effects model
##
## Q df p-value tau.within tau2.within
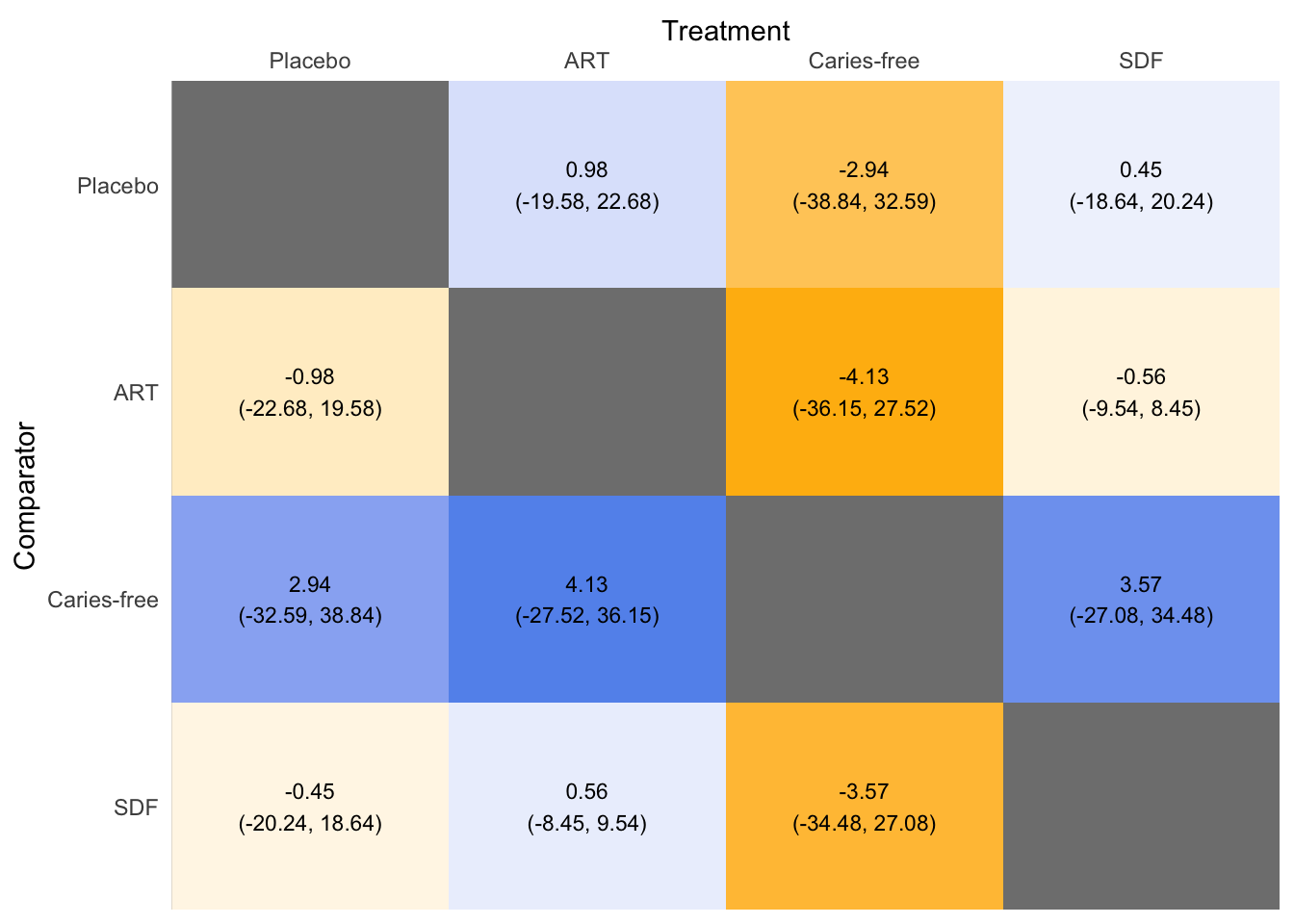
## Between designs 0.00 0 -- 0 0次の図はあまり必要ないかもしれない。直接か間接かを示します。
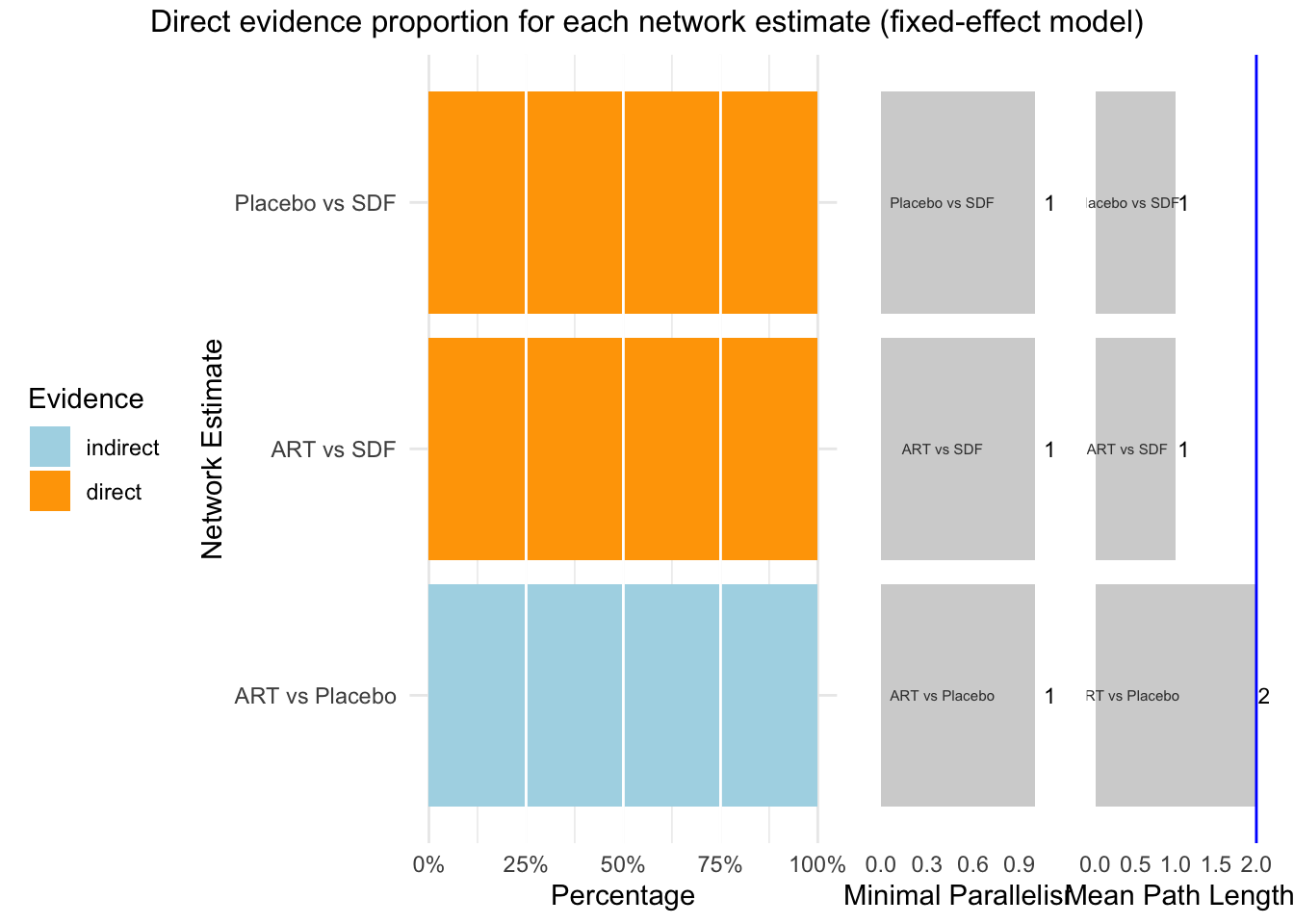
## Separate indirect from direct evidence (SIDE) using back-calculation method
##
## Common effects model:
##
## comparison k prop nma direct indir. Diff z p-value
## ART vs Placebo 0 0 -0.011 . -0.011 . . .
## ART vs SDF 2 1.00 0.018 0.018 . . . .
## Placebo vs SDF 2 1.00 0.028 0.028 . . . .
##
## Legend:
## comparison - Treatment comparison
## k - Number of studies providing direct evidence
## prop - Direct evidence proportion
## nma - Estimated treatment effect (SMD) in network meta-analysis
## direct - Estimated treatment effect (SMD) derived from direct evidence
## indir. - Estimated treatment effect (SMD) derived from indirect evidence
## Diff - Difference between direct and indirect treatment estimates
## z - z-value of test for disagreement (direct versus indirect)
## p-value - p-value of test for disagreement (direct versus indirect)p < 0.05 であると、非一貫である。
3.3 gemtc ベイズ
{gemtc} を使う場合には、４つの決まって列を持つデータフレームをあらかじめ準備する必要がある。
library(meta)
metaRuff2022gemtc <- metacont(
n.e = Ne,
mean.e = Me,
sd.e = Se,
n.c = Nc,
mean.c = Mc,
sd.c = Sc,
studlab = studlab,
data = dfRuff2022,
sm = "SMD",
fixed = FALSE,
label.e = "Experimental",
label.c = "Control")library(data.table)
dfMtcRuff2022 <- data.table(
study = metaRuff2022gemtc$studlab,
diff = metaRuff2022gemtc$TE,
std.err = metaRuff2022gemtc$seTE,
treatment = metaRuff2022gemtc$data$treat)
dfMtcRuff2022_2 <- data.table(
study = metaRuff2022gemtc$studlab,
diff = NA,
std.err = NA,
treatment = metaRuff2022gemtc$data$control)
dfMtcRuff2022 <- rbind(dfMtcRuff2022, dfMtcRuff2022_2)treatment では + や - など記号はダメらしい。許されているのは _ だけなので、置換する。
dfMtcRuff2022$treatment <- sub("\\+", "_", dfMtcRuff2022$treatment)
dfMtcRuff2022$treatment <- sub("\\-", "_", dfMtcRuff2022$treatment)
#dfMtcRuff2022$treatment <- sub("\\/", "_", dfMtcRuff2022$treatment)## $Description
## [1] "MTC dataset: Network"
##
## $`Studies per treatment`
## ART Caries_free Placebo SDF
## 2 1 2 5
##
## $`Number of n-arm studies`
## 2-arm
## 5
##
## $`Studies per treatment comparison`
## t1 t2 nr
## 1 ART SDF 2
## 2 Caries_free SDF 1
## 3 Placebo SDF 2
3.3.3 モデル実行
## Compiling model graph
## Resolving undeclared variables
## Allocating nodes
## Graph information:
## Observed stochastic nodes: 5
## Unobserved stochastic nodes: 3
## Total graph size: 84
##
## Initializing model##
## Results on the Mean Difference scale
##
## Iterations = 10:10000
## Thinning interval = 10
## Number of chains = 4
## Sample size per chain = 1000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## d.SDF.ART 0.01463 0.17406 0.002752 0.002828
## d.SDF.Caries_free -0.71483 0.12399 0.001960 0.001950
## d.SDF.Placebo 0.02803 0.09383 0.001484 0.001493
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## d.SDF.ART -0.3228 -0.10259 0.01688 0.13280 0.3533
## d.SDF.Caries_free -0.9657 -0.79915 -0.71376 -0.63186 -0.4733
## d.SDF.Placebo -0.1511 -0.03715 0.02788 0.09365 0.2143
##
## -- Model fit (residual deviance):
##
## Dbar pD DIC
## 3.006444 2.963083 5.969527
##
## 5 data points, ratio 0.6013, I^2 = 0%## Compiling model graph
## Resolving undeclared variables
## Allocating nodes
## Graph information:
## Observed stochastic nodes: 5
## Unobserved stochastic nodes: 9
## Total graph size: 106
##
## Initializing model##
## Results on the Mean Difference scale
##
## Iterations = 5010:15000
## Thinning interval = 10
## Number of chains = 4
## Sample size per chain = 1000
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## d.SDF.ART 0.01947 0.2693 0.004258 0.004670
## d.SDF.Caries_free -0.71724 0.2970 0.004696 0.004771
## d.SDF.Placebo 0.02970 0.2143 0.003388 0.003578
## sd.d 0.20652 0.1753 0.002771 0.004201
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## d.SDF.ART -0.509240 -0.13944 0.01327 0.1737 0.5914
## d.SDF.Caries_free -1.376002 -0.85521 -0.71703 -0.5786 -0.0818
## d.SDF.Placebo -0.432068 -0.07765 0.03223 0.1350 0.4751
## sd.d 0.007148 0.06827 0.15185 0.3045 0.6434
##
## -- Model fit (residual deviance):
##
## Dbar pD DIC
## 3.813690 3.792071 7.605760
##
## 5 data points, ratio 0.7627, I^2 = 0%
3.3.6 一貫性の評価
Node split は、論文中でも未対応。
実行するとしたら、以下のように行う。
nodesplit <- mtc.nodesplit(mtcNetwork,
linearModel = "random",
likelihood = "normal",
link = "identity",
n.adapt = 5000,
n.iter = 1e5,
thin = 10)
plot(summary(nodesplit))2.3 Data synthesis
… Node split analyses were not performed due to the small number of studies included in analysis.
もし行う場合は、以下のようなコードになる（この場合はエラーになる）。
3.4 BUGSnet ベイズ
{meta} パッケージのデータフレームは、1行に介入群と参照群がある contrast-based であった。
{BUGSnet} パッケージは、1行に１群の arm-based である必要がある。studlab が同じ複数行を一つの研究と認識する。
gemtc も arm-based としたが、BUGSnet の arm-based とは異なる。
treatment 列には治療方法、M 列には平均値、S 列には標準偏差、N 列にはサンプルサイズを格納する。
## ── Attaching packages ────────
## ✔ ggplot2 3.4.0 ✔ purrr 1.0.1
## ✔ tibble 3.1.8 ✔ dplyr 1.0.10
## ✔ tidyr 1.2.1 ✔ stringr 1.5.0
## ✔ readr 2.1.3 ✔ forcats 0.5.2
## ── Conflicts ─────────────────
## ✖ dplyr::between() masks data.table::between()
## ✖ tidyr::expand() masks Matrix::expand()
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::first() masks data.table::first()
## ✖ dplyr::lag() masks stats::lag()
## ✖ dplyr::last() masks data.table::last()
## ✖ tidyr::pack() masks Matrix::pack()
## ✖ purrr::transpose() masks data.table::transpose()
## ✖ tidyr::unpack() masks Matrix::unpack()df1_a<-pivot_longer(dfRuff2022, cols=c(treat, control),
names_to = "varname_t")
df1_b <- df1_a[,c("studlab", "varname_t", "Me", "Se", "Ne", "Mc", "Sc", "Nc", "value")]
df1_b <- mutate(df1_b, treatment = value)
df1_b <- mutate(df1_b, M = ifelse(varname_t == "control", Mc, Me))
df1_b <- mutate(df1_b, S = ifelse(varname_t == "control", Nc, Ne))
df1_b <- mutate(df1_b, N = ifelse(varname_t == "control", Nc, Ne))
dfBUGS <- df1_b[,c("studlab", "treatment", "M", "S", "N")]以下のようにデータフレームが変更された。
library(BUGSnet)
myBUGObject <- data.prep(arm.data = dfBUGS,
varname.t = "treatment",
varname.s = "studlab")
3.4.2 要約
myBUGNetwork <- net.tab(data = myBUGObject,
outcome = "M",
N = "N",
type.outcome = "continuous",
time = NULL)
myBUGNetwork$intervention## # A tibble: 4 × 6
## treatment n.studies n.patients min.outcome max.outcome av.outcome
## <chr> <int> <int> <dbl> <dbl> <dbl>
## 1 ART 2 67 4.5 6.94 6.47
## 2 Caries-free 1 152 2.5 2.5 2.5
## 3 Placebo 2 219 6.3 7.1 6.63
## 4 SDF 5 411 3.9 6.94 6.333.4.3 モデル作成
主要な統計分析を行う。
BugsModelFixed <- nma.model(data=myBUGObject,
outcome="M",
sd = "S",
N="N",
reference="Placebo",
family="normal",
link = "identity",
effects="fixed")
BugsModelRandom <- nma.model(data=myBUGObject,
outcome="M",
sd = "S",
N="N",
reference="Placebo",
family="normal",
link = "identity",
effects="random")3.4.4 モデル実行
set.seed(20190829)
BugsResFixed <- nma.run(BugsModelFixed,
n.adapt=1000,
n.burnin=1000,
n.iter=10000)## Compiling model graph
## Resolving undeclared variables
## Allocating nodes
## Graph information:
## Observed stochastic nodes: 10
## Unobserved stochastic nodes: 8
## Total graph size: 113
##
## Initializing model## Compiling model graph
## Resolving undeclared variables
## Allocating nodes
## Graph information:
## Observed stochastic nodes: 10
## Unobserved stochastic nodes: 14
## Total graph size: 133
##
## Initializing model3.4.5 収束の評価
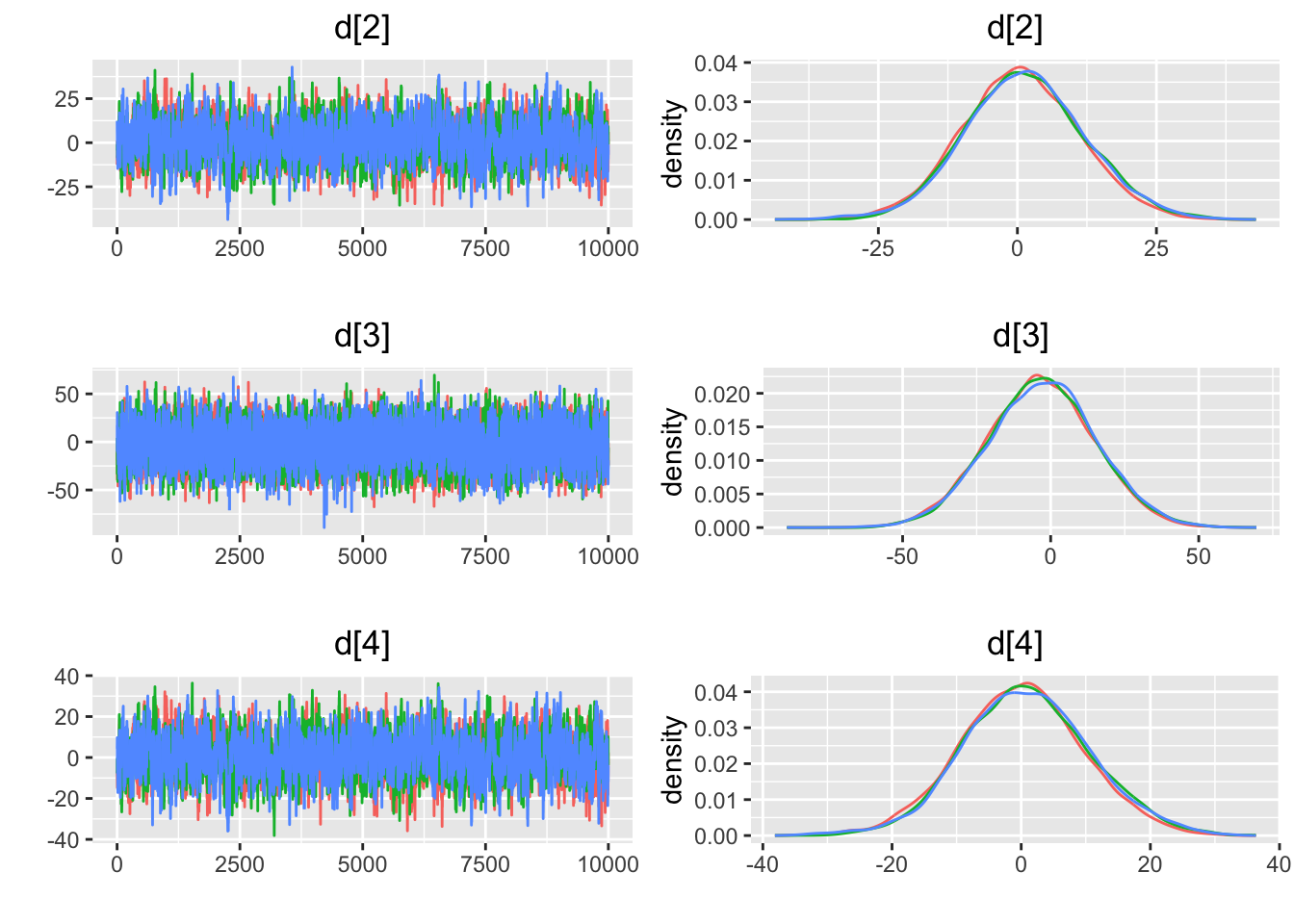
## $gelman.rubin
## $psrf
## Point est. Upper C.I.
## d[2] 1.004762 1.016807
## d[3] 1.001656 1.006173
## d[4] 1.005496 1.019319
##
## $mpsrf
## [1] 1.005109
##
## attr(,"class")
## [1] "gelman.rubin.results"
##
## $geweke
## $stats
## Chain 1 Chain 2 Chain 3
## d[2] 0.10339572 0.2323212 0.5195570
## d[3] -0.96359782 0.2283794 0.3587106
## d[4] 0.02249617 0.2867542 0.3285498
##
## $frac1
## [1] 0.1
##
## $frac2
## [1] 0.5
##
## attr(,"class")
## [1] "geweke.results"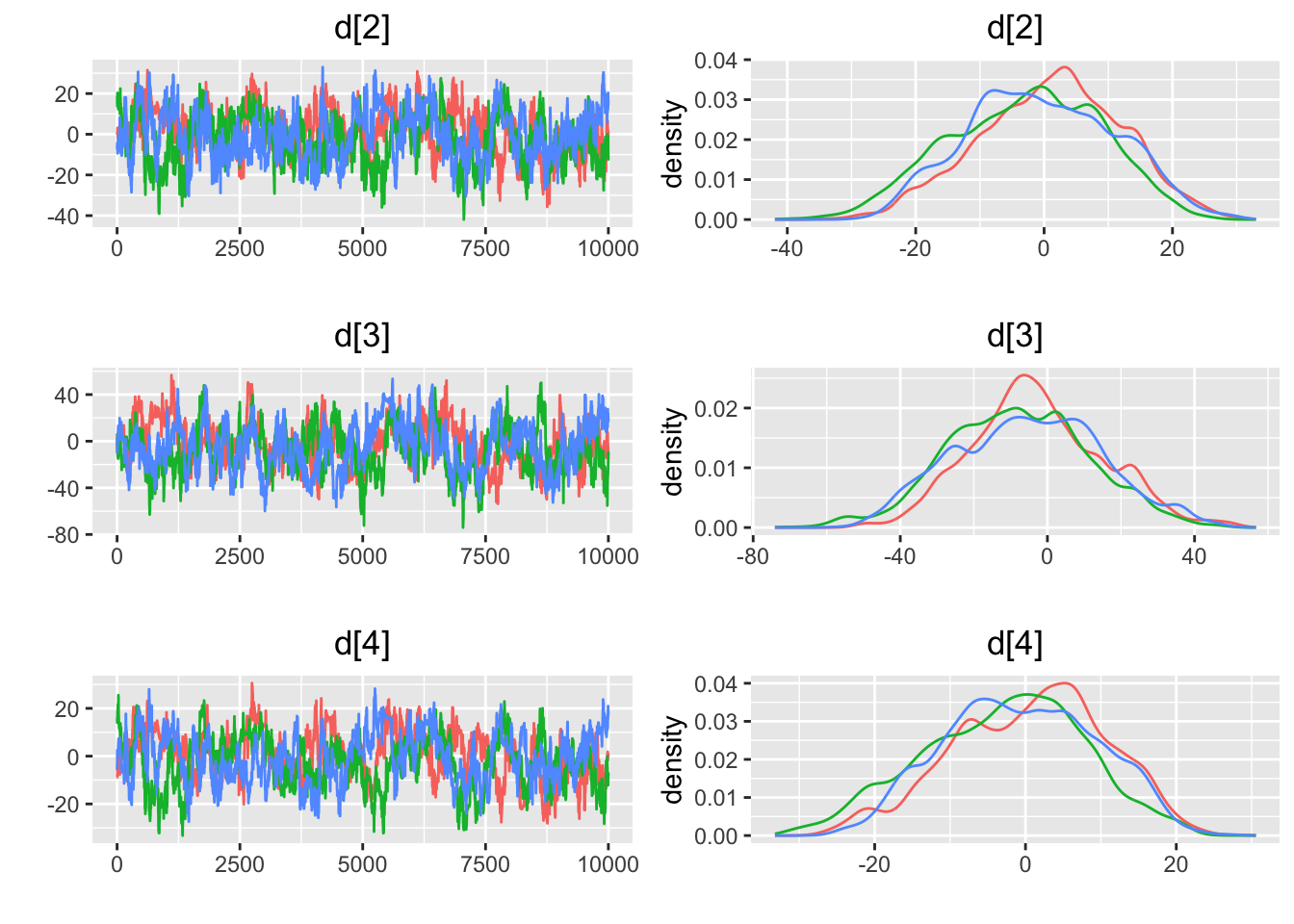
## Press [ENTER] to continue plotting trace plots (or type 'stop' to end plotting)>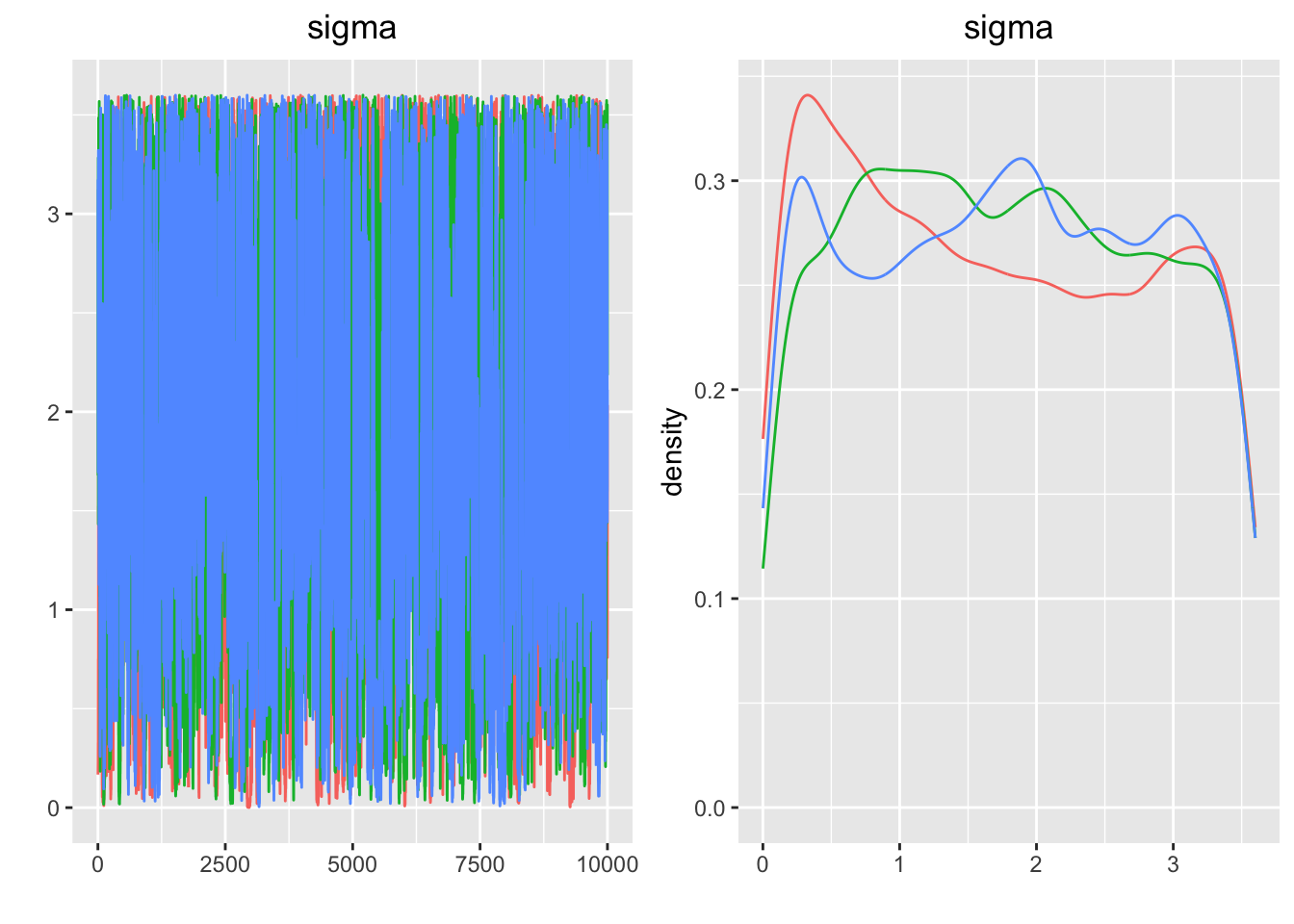
## $gelman.rubin
## $psrf
## Point est. Upper C.I.
## d[2] 1.032429 1.110878
## d[3] 1.025559 1.076214
## d[4] 1.043298 1.145424
## sigma 1.000649 1.000827
##
## $mpsrf
## [1] 1.038573
##
## attr(,"class")
## [1] "gelman.rubin.results"
##
## $geweke
## $stats
## Chain 1 Chain 2 Chain 3
## d[2] 2.766882 0.153567116 0.2735423
## d[3] 2.405083 -0.477477778 -1.7087371
## d[4] 2.176869 -0.009129389 0.1156472
## sigma -1.690940 0.782471349 0.5353383
##
## $frac1
## [1] 0.1
##
## $frac2
## [1] 0.5
##
## attr(,"class")
## [1] "geweke.results"3.4.6 適合度の評価
モデルの適合度を評価します。
## $DIC
## [1] 15.40845
##
## $Dres
## [1] 7.708799
##
## $pD
## [1] 7.699648
##
## $leverage
##
## 1 0.7534557 0.6611159 0.9274778 0.5848702 0.89628 0.7428806 0.6986818 0.9465668
##
## 1 0.5876678 0.9006518
##
## $w
## y.1.1. y.2.1. y.3.1. y.4.1. y.5.1. y.1.2. y.2.2.
## 0.8695872 0.8143781 0.9630654 -0.7655618 0.9467267 -0.8623771 -0.8361831
## y.3.2. y.4.2. y.5.2.
## 0.9729347 0.7676466 -0.9490809
##
## $pmdev
## dev_a.1.1. dev_a.2.1. dev_a.3.1. dev_a.4.1. dev_a.5.1. dev_a.1.2. dev_a.2.2.
## 0.7561818 0.6632117 0.9274949 0.5860848 0.8962914 0.7436943 0.6992022
## dev_a.3.2. dev_a.4.2. dev_a.5.2.
## 0.9466019 0.5892814 0.9007546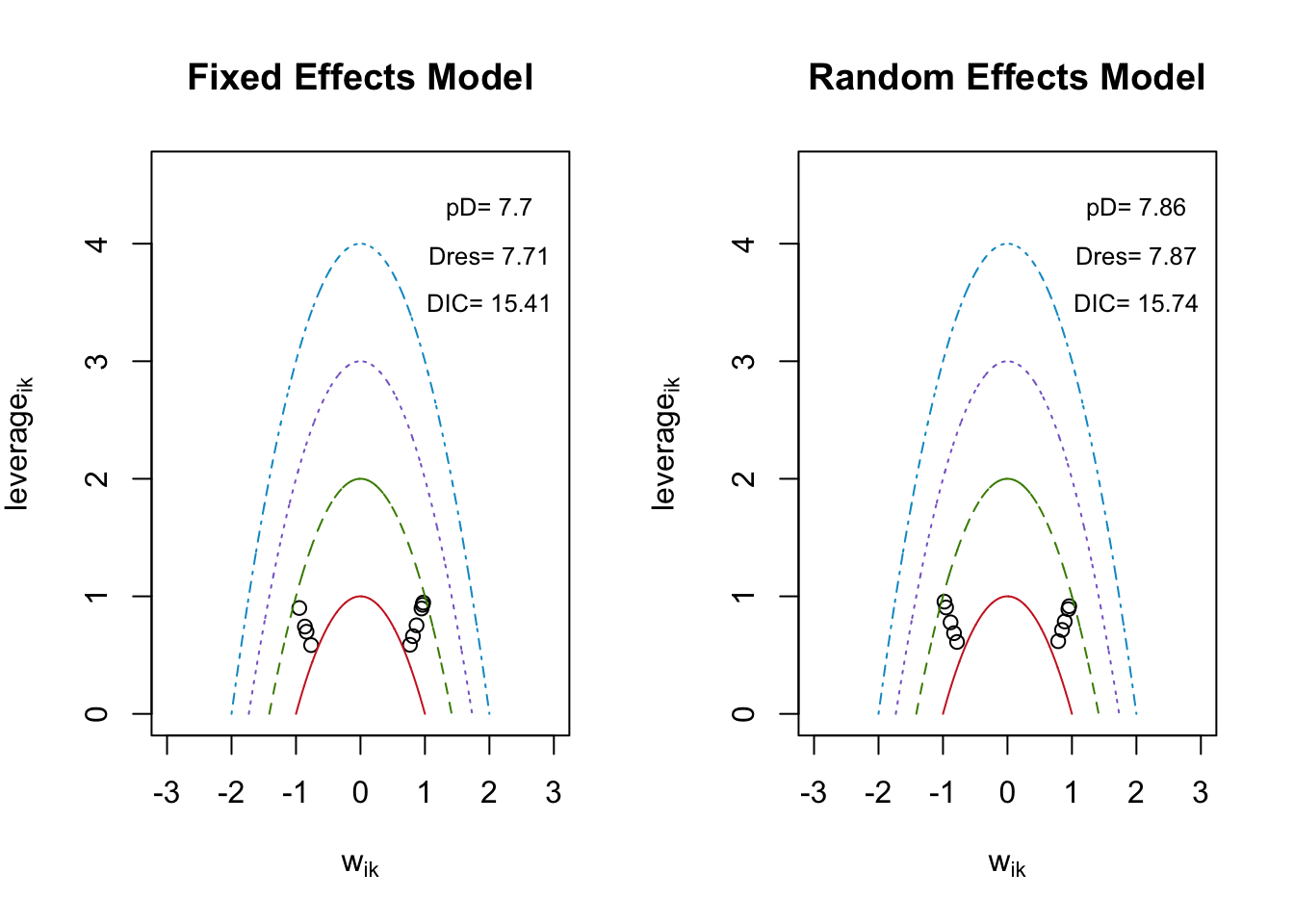
## $DIC
## [1] 15.73608
##
## $Dres
## [1] 7.874658
##
## $pD
## [1] 7.861423
##
## $leverage
##
## 1 0.7786832 0.6865626 0.9159764 0.6118047 0.8903945 0.7858494 0.7142104
##
## 1 0.9548114 0.6181272 0.9050033
##
## $w
## y.1.1. y.2.1. y.3.1. y.4.1. y.5.1. y.1.2. y.2.2.
## -0.8828966 -0.8288923 0.9576618 -0.7821811 0.9448657 0.8880589 0.8464517
## y.3.2. y.4.2. y.5.2.
## -0.9774147 0.7868512 -0.9522557
##
## $pmdev
## dev_a.1.1. dev_a.2.1. dev_a.3.1. dev_a.4.1. dev_a.5.1. dev_a.1.2. dev_a.2.2.
## 0.7795063 0.6870624 0.9171161 0.6118073 0.8927712 0.7886486 0.7164804
## dev_a.3.2. dev_a.4.2. dev_a.5.2.
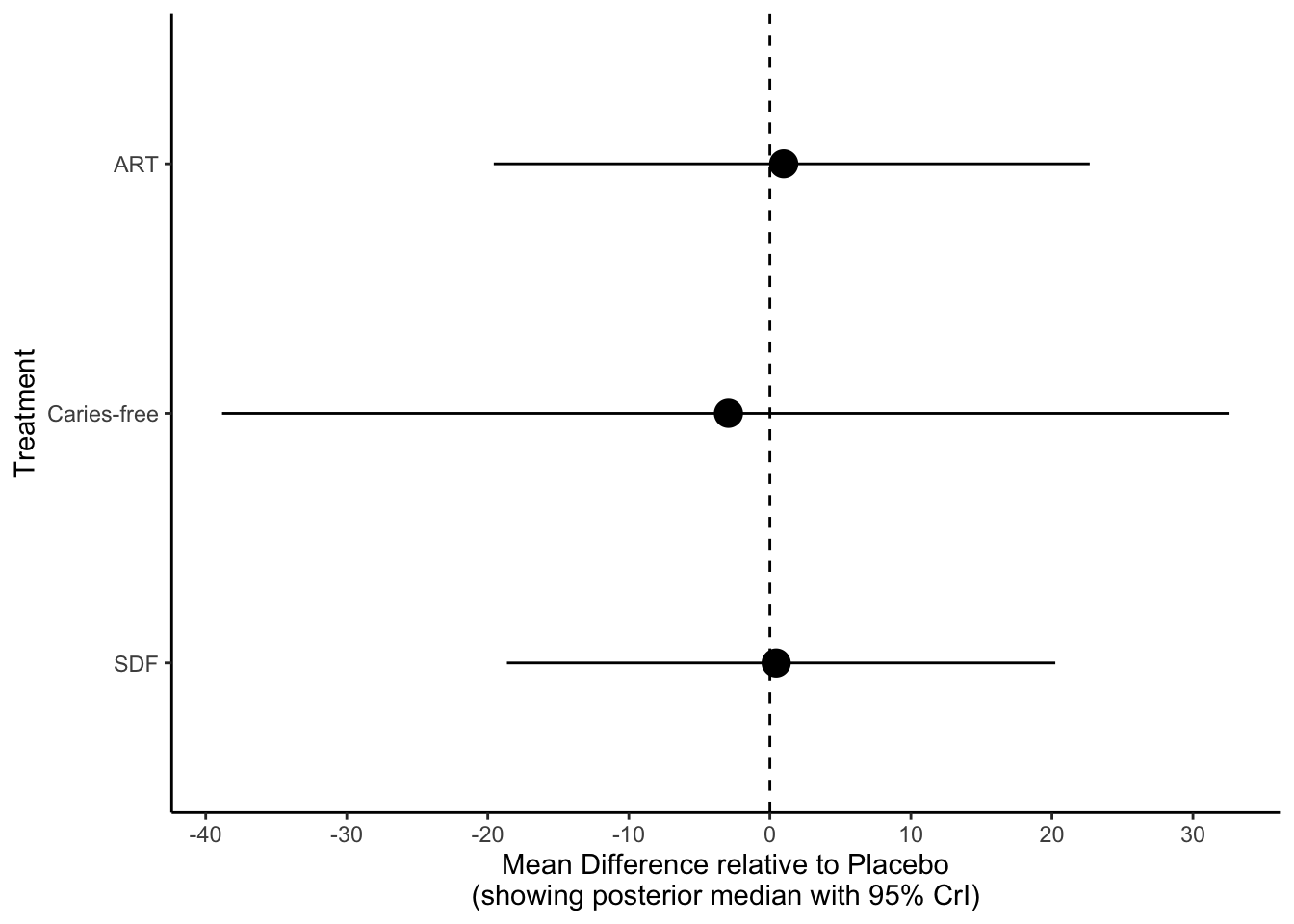
## 0.9553395 0.6191347 0.9067910DIC 値が低いほど、適合度が高い。固定効果とランダム効果の DIC 値の差はわずかだが、固定効果の方が良さそうである。
References
Ruff, Ryan Richard, Rachel Whittemore, Martyna Grochecki, Jillian Bateson, and Tamarinda J Barry Godı́n. 2022. “Silver Diamine Fluoride and Oral Health-Related Quality of Life: A Review and Network Meta-Analysis.” PloS One 17 (2): e0261627.