Chapter 11 スクリプト、アルゴリズム、関数 | Geocomputation with R

Robin Lovelace; Jakub Nowosad; Jannes Muenchow

11 スクリプト、アルゴリズム、関数

必須パッケージ

この章では、主に Base R を使用するため、必要なソフトウェアは最小限である。これから開発するアルゴリズムの結果を確認するために sf パッケージだけを使用する。 Chapter 2 で紹介した地理クラスと、それを使ってさまざまな入力ファイル形式を表現する方法 (Chapter 8 参照) について理解していることを前提にしている。

11.1 イントロダクション

Chapter 1 は、ジオコンピュテーションは既存のツールを使うだけでなく、「共有可能な R スクリプトや関数の形で」新しいツールを開発することが重要であることを示した。本章では、これらの再現性のあるコードの構成要素について学ぶ。また、Chapter 10 で使用されているような低レベルの幾何学的アルゴリズムも紹介する。これを読めば、このようなアルゴリズムの仕組みを理解し、複数のデータセットに対して、多くの人が、何度も使えるようなコードを書くことができるようになるはずである。本章だけでは、熟練したプログラマになることはできない。プログラミングは難しく、十分な練習が必要である (Abelson, Sussman, and Sussman 1996) :

プログラミングをそれ自体の知的活動として理解するためには、プログラミングに目を向けなければならないし、プログラムを読み、書かなければならない。

しかし、プログラミングを学ぶ強い理由がある。この章では、プログラミングそのものを教えるわけではない。プログラミングについては、Wickham (2019)、Gillespie and Lovelace (2016)、Xiao (2016) を推奨する。これらの書籍は R や他の言語について教えてくれる。また、地理データに焦点を当て、プログラミング能力を伸ばすための基礎を作ることができる。

本章は、再現性の重要性について、例を示しながら強調していきたい。再現性の利点は、他の人があなたの研究を複製することを可能にするだけではない。再現性のあるコードは、一度だけ実行されるように書かれたコードよりも、計算効率、スケーラビリティ (より大きなデータセットに対して実行するコードの能力)、適応やメンテナンスのしやすさなど、あらゆる面で優れていることが多いのである。

スクリプトは、再現可能な R コードの基礎であり、このトピックは、Section 11.2 でカバーされている。アルゴリズムは、Section 11.3 で説明されているように、一連のステップを使用して入力を変更し、その結果、出力を得るためのレシピである。共有と再現を容易にするために、アルゴリズムを関数に配置することができる。それが、Section 11.4 のトピックである。ポリゴンの重心を求める例で、これらの概念を結びつけていこう。 Chapter 5 で、重心の関数 st_centroid() をすでに紹介したが、この例は、一見単純な操作が比較的複雑なコードの結果であることを強調し、次の観察を保証する (Wise 2001) 。

空間データの問題で最も興味深いのは、人間にとっては些細なことに見えることが、コンピュータにとっては驚くほど難しいということである。

この例は、Xiao (2016) にならい、「世の中にあるものを複製するのではなく、世の中のものがどのように機能しているかを示す」という本章の第二の目的も反映している。

11.2 スクリプト

パッケージで配布される関数が R コードの構成要素だとすれば、スクリプトはそれらを論理的な順序でまとめる接着剤となる。スクリプトとは、再現可能なワークフローを作り出す目的で、手動または targets などの自動化ツールで保存・実行される (Landau 2021)。プログラミングの初心者にとってスクリプトは敷居が高く聞こえるかもしれないが、単なるプレーンテキストファイルである。スクリプトは、通常はその言語を表す拡張子で保存される。例えば、Python は .py、Rust は .rs である。 R スクリプトは一般に、.R 拡張子で保存され、実行内容を反映した名前が付けられる。例として、この本のリポジトリの code フォルダに格納されているスクリプトファイル 11-hello.R がある。 11-hello.R は、次の 2 行のコードが含まれているだけの簡単なスクリプトで、そのうち 1 行はコメントである。

# Aim: provide a minimal R script
print("Hello geocompr")

このスクリプトの中身は、とりたててスゴいものではないが、「スクリプトは複雑である必要はない」という点を示している。保存されたスクリプトは、source() を使って、その全体を呼び出したり、実行したりすることができる。このコマンドの出力から、コメント行は無視され、print() コマンドが実行されることがわかる。

source("code/11-hello.R")
#> [1] "Hello geocompr"

以下のように bash や PowerShell などのシステムコマンドラインシェルから R スクリプトを呼び出すこともできる。

Rscript code/11-hello.R

RScript 実行可能ファイルが設定されていれば、システムのシェルで Hello geocompr と表示される。スクリプトファイルに何を書くべきで何を書くべきではないかについて厳密なルールがあるわけではない。壊れた再現性のないコードになることもよくあるので、テストが必要である。有効な R を含まないコード行は、エラーを防ぐため、行頭に # を追加してコメントアウトする必要がある。11-hello.R スクリプトの 1 行目を参照。守るべき基本的ルールもある。

順番に書く。映画の脚本と同じように、スクリプトも「設定」「データ処理」「結果保存」といった明確な順番が必要である (映画でいうところの「始まり」「中間」「終わり」にほぼ相当する)
他の人 (と未来の自分) が理解できるように、スクリプトにコメントを追加してみよう。これは、例えば、RStudio で、「折りたたみ可能な」コードセクションの見出しを作成するショートカット Ctrl+Shift+R を使って行うことができる
特に、スクリプトは再現可能であるべきである。どんなコンピュータでも動作する自己完結型のスクリプトは、調子の良い日に自分のコンピュータでしか動作しないスクリプトよりも有用である。これには、必要なパッケージを最初に添付し、データを永続的なソース (信頼できるウェブサイトなど) から読み込み、前のステップが実行されたことを確認することが含まれる。⁷⁸

パッケージ化しないかいぎり R スクリプトで再現性を強制するのは難しいが、それを助けるツールはある。 RStudio は、デフォルトで R スクリプトを「コードチェック」し、不具合のあるコードに赤い波線を引く (下図参照)。 repex パッケージは、再現性のためのツールである。

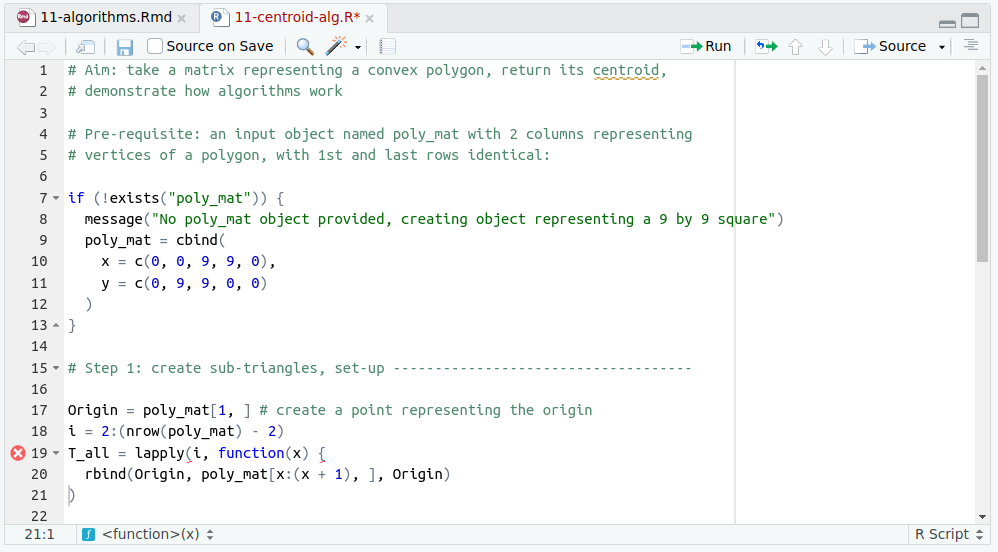
FIGURE 11.1: RStudio でのコード確認の様子。この例は 11-centroid-alg.R スクリプトの 19 行目のカッコが閉じられていないことを示している。

再現性に役立つのは reprex パッケージである。このパッケージの reprex() 関数は、R コードが再現可能かどうかを確認し、GitHub などのサイトで交流する際に使えるマークダウンを生成する。詳細は reprex.tidyverse.org を参照。

このセクションの内容は、あらゆるタイプの R スクリプトに適用できる。ジオコンピュテーションのためのスクリプトで特に考慮すべき点は、GDAL など外部ライブラリへの依存が多い点である。実際、Chapter 8 のデータ入出力では GDAL をたくさん使用した。 GIS ソフトウェアの依存は、Chaptger 10 で解説したようにより多くの特別なジオアルゴリズムを実行するために必要になる。地理データを扱うスクリプトは、入力データセットが特定のファイル形式であることを必要とする。このような依存関係は、スクリプトのコメントとして、またはスクリプトの一部であるプロジェクトの他の場所でコメントするか、renv や Docker などで依存性として記述するべきである。

「保守的」プログラミング技術と適切なエラーメッセージは、要件が満たされていない時に依存性を確認し、ユーザと対話する時間を節約する。 R では if () で表される If 文を使用し、特定の条件が揃った時のみにメッセージを送ったりコードを実行するようにコードを書く。以下のコード例は、特定のファイルがない場合にユーザにメッセージを送る (訳註: メッセージに日本語を使わないことを推奨する。)。

if (!file.exists("required_geo_data.gpkg")) {
  message("No file, required_geo_data.gpkg is missing!")
} 
#> No file, required_geo_data.gpkg is missing!

このスクリプトが行う作業は、以下の再現例で示されている。このスクリプトは、poly_mat という、長さ 9 単位の辺を持つ正方形 (この意味は次のセクションで明らかになる) という前提条件のオブジェクトに対して動作する。この例では、インターネットに接続していることを前提に、source() が URL (ここでは短縮版を使用) で動作することを示している。そうでない場合は、github.com/geocompx/geocompr からダウンロードできる geocompr フォルダのルートディレクトリから R を実行していると仮定して、source("code/11-centroid-alg.R") で同じスクリプトを呼び出すことができる。

poly_mat = cbind(
  x = c(0, 9, 9, 0, 0),
  y = c(0, 0, 9, 9, 0)
)
# geocompr リポジトリの code/11-centroid-alg.R の短い URL
source("https://t.ly/0nzj")

#> [1] "The area is: 81"
#> [1] "The coordinates of the centroid are: 4.5, 4.5"

11.3 幾何学的アルゴリズム

アルゴリズムは、コンピュータにおける料理のレシピに相当するものと理解することができる。入力に対して実行されると、有用または美味しい出力が得られる指示の完全なセットである。入力とは、料理においては小麦粉や砂糖などの食材で、アルゴリズムの場合はデータと入力パラメータとなる。美味しいケーキはレシピの結果であるのと同様に、アルゴリズムの成功は環境や社会的に利点のある出力となりうる。具体的なケーススタディに入る前に、アルゴリズムとスクリプト (Section 11.2 ) や関数 (Section 11.4 で説明するように、アルゴリズムを一般化し、他でも使えるようにしたり簡単にする) の関係について簡単に説明する。

「アルゴリズム」という言葉は、西暦825年のバグダッドで出版されたされた、初期の数学教科書に端を発している。この本はラテン語に翻訳され、人気を博しただけでなく、著者の名字である al-Khwārizmī が「科学用語として不滅の名声を得て、Alchoarismi、Algorismi、そして最終的には algorithm になった」 (Bellos 2011) 。コンピュータ時代には、アルゴリズムは、問題を解決する一連のステップを指し、その結果、あらかじめ定義された出力が得られる。入力は、適切なデータ構造で正式に定義されなければならない (Wise 2001)。アルゴリズムは、多くの場合、コードで実装される前に、処理の目的を示すフローチャートや疑似コードとして開始される。使い勝手をよくするために、一般的なアルゴリズムは関数内にパッケージ化されていることが多く、(関数のソースコードを見ない限り) 一部または全部の手順が隠されている場合がある (Section 11.4 を参照)。

Chapter 10 で見たようなジオアルゴリズムは、地理的なデータを取り込み、一般的には地理的な結果を返すアルゴリズムである (同じものを表す別の用語として、GIS アルゴリズム、幾何学的アルゴリズムがある)。簡単そうに聞こえるだろうが、このテーマは奥が深く、計算幾何学という学問分野全体がその研究に専念している (Berg et al. 2008)。このテーマに関する書籍も多数出版されている。例えば、O’Rourke (1998) は、再現可能で自由に利用できる C コードを用いて、徐々に難しくなる幾何学的アルゴリズムの範囲を紹介している。

幾何学的アルゴリズムの例としては、ポリゴンの重心を求めるものがある。重心の計算には多くのアプローチがあり、中には特定のタイプの空間データに対してのみ機能するものもある。本節では、視覚化しやすいアプローチを選択する。ポリゴンを多くの三角形に分割し、それぞれの重心を求める。このアプローチは、他の重心アルゴリズムと並んで Kaiser and Morin (1993) によって議論された (簡単な説明は O’Rourke 1998)。コードを書く前に、このアプローチをさらに個別のタスクに分解するのに役立つ (以降、ステップ 1 からステップ 4 と呼ぶが、これらは模式図や疑似コードとして提示すこともできる)。

ポリゴンを連続した三角形に分割する
各三角形の重心を求める
それぞれの三角形の面積を求める
三角形の中心点の面積加重平均を求める

一見、簡単そうに見えるが、言葉をコードに変換するには、入力に制約がある場合でも、試行錯誤を繰り返しながら作業を進める必要がある。このアルゴリズムは、180°以上の内角を持たない凸ポリゴンに対してのみ動作し、星形は使用できない (パッケージの decido と sfdct は外部ライブラリを使用して非凸ポリゴンを三角測量できる。geocompx.org の algorithm vignetteに示されている。)。

ポリゴンの最も単純なデータ構造は、x と y の座標の行列で、各行はポリゴンの境界を順にたどる頂点を表し、最初と最後の行は同一である (Wise 2001)。今回は、GIS Algorithms (Xiao 2016 Python コードは github.com/gisalgs を参照) の例を参考に、Figure 11.2 に示すように、5 つの頂点を持つポリゴンを Base R で作成する。

# ポリゴンを表現する行列を作成
x_coords = c(10, 20, 12, 0, 0, 10)
y_coords = c(0, 15, 20, 10, 0, 0)
poly_mat = cbind(x_coords, y_coords)

これで、例となるデータセットができたので、上記のステップ 1 に着手する準備が整った。以下のコードでは、1 つの三角形 (T1) を作成して、この方法を示している。また、数式 \(1/3(a + b + c)\) (\(a\) から \(c\) は三角形の頂点を表す座標) に基づいて重心を計算するステップ 2 も示している。

# 原点を作成:
Origin = poly_mat[1, ]
# 三角形の行列を作成:
T1 = rbind(Origin, poly_mat[2:3, ], Origin) 
C1 = (T1[1,] + T1[2,] + T1[3,]) / 3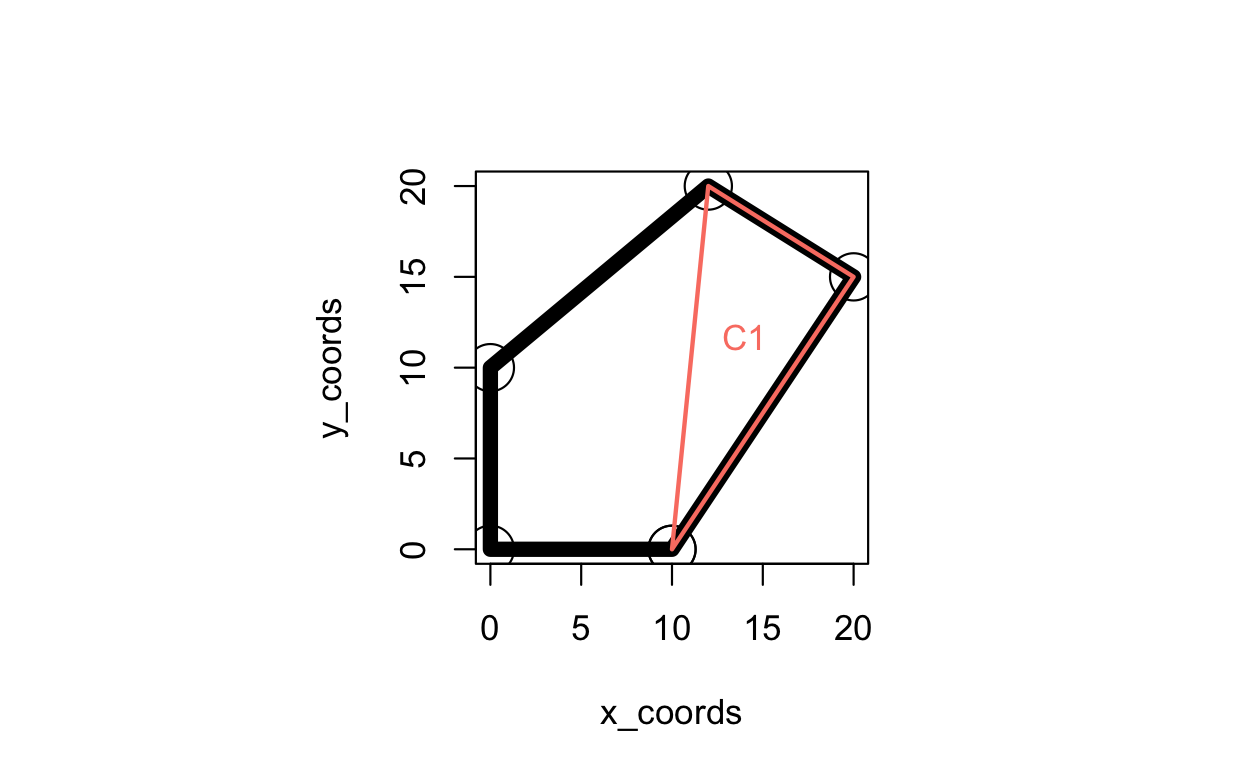

FIGURE 11.2: ポリゴン重心計算問題。

ステップ 3 では、各三角形の面積を求めるので、大きな三角形の不釣り合いな影響を考慮した加重平均を計算する。三角形の面積を計算する公式は次の通りである (Kaiser and Morin 1993)。

\[ \frac{A_x ( B_y − C_y ) + B_x ( C_y − A_y ) + C_x ( A_y − B_y )}{ 2 } \]

ここで、\(A\) から \(C\) は三角形 T1 の 3 点、\(x\) と \(y\) は x と y の次元を指す。この式を、三角形の行列表現のデータを扱う R コードに翻訳すると、次のようになる (関数 abs() は、正の結果を保証する)。

# 行列 T1 で表される三角形の面積を計算
abs(T1[1, 1] * (T1[2, 2] - T1[3, 2]) +
    T1[2, 1] * (T1[3, 2] - T1[1, 2]) +
    T1[3, 1] * (T1[1, 2] - T1[2, 2])) / 2
#> [1] 85

このコードチャンクは正しい結果を出力する。⁷⁹ このコードは不格好で、別の三角行列で実行する場合、再入力しなければならない点が問題である。より一般化するために、このコードを Section 11.4 で関数に変換する方法を見てみよう。

ステップ 4 では、ステップ 2 と 3 を 1 つの三角形だけでなく、すべての三角形に対して行う必要がある (上の例)。このため、ポリゴンを表すすべての三角形を作成するためのイテレーション (繰り返し) が必要である。Figure 11.3 に示す。 lapply() と vapply() が各三角形の反復処理に使われているのは、Base R で簡潔な解が得られるからである。⁸⁰

i = 2:(nrow(poly_mat) - 2)
T_all = lapply(i, function(x) {
  rbind(Origin, poly_mat[x:(x + 1), ], Origin)
})

C_list = lapply(T_all,  function(x) (x[1, ] + x[2, ] + x[3, ]) / 3)
C = do.call(rbind, C_list)

A = vapply(T_all, function(x) {
  abs(x[1, 1] * (x[2, 2] - x[3, 2]) +
        x[2, 1] * (x[3, 2] - x[1, 2]) +
        x[3, 1] * (x[1, 2] - x[2, 2]) ) / 2
  }, FUN.VALUE = double(1))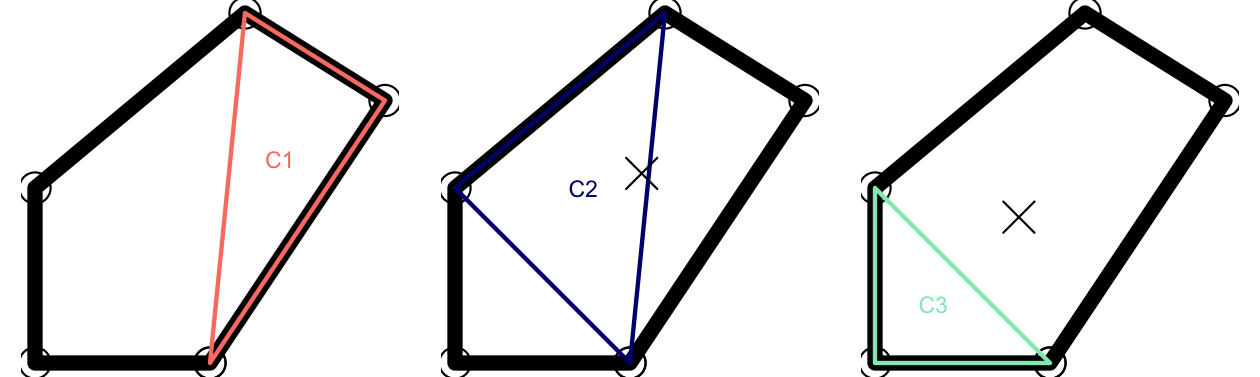

FIGURE 11.3: 複数の三角による繰り返し重心アルゴリズム。繰り返し 2 と 3 における X は、面積加重重心。

これで、ステップ 4 を完了し、総面積を sum(A) で計算し、ポリゴンの重心座標を weighted.mean(C [, 1] , A) と weighted.mean(C [, 2] , A) でポリゴンの重心座標を計算する (注意深い読者のための練習: これらのコマンドが動作することを確認してみよう)。アルゴリズムとスクリプトの関連性を示すために、このセクションの内容を凝縮して 11-centroid-alg.R とした。 Section 11.2 の最後で、このスクリプトが正方形の重心を計算する方法を見た。アルゴリズムをスクリプト化することの素晴らしい点は、新しい poly_mat オブジェクト上で動作することである (st_centroid() を参照してこれらの結果を検証するには、以下の演習を参照)。

source("code/11-centroid-alg.R")
#> [1] "The area is: 245"
#> [1] "The coordinates of the centroid are: 8.83, 9.22"

上記の例では、低レベルの地理的な操作は、base R で第一原理から開発することができることが示されている。また、すでに試行錯誤したソリューションが存在する場合、車輪の再発明をする価値はないことも示している。もし、ポリゴンの重心を求めるだけなら、poly_mat を sf オブジェクトとして表現し、代わりに既存の sf::st_centroid() 関数を使用する方が早かっただろう。しかし、第一原理でアルゴリズムを書くことの大きな利点は、プロセスのすべての段階を理解できることであり、他の人のコードを使うときには保証されないことである。さらに考慮すべきは性能である。R は C++ のような低レベルの言語と比較すると数値計算が遅いことが多く、最適化が困難である (Section 1.4 参照)。新しい手法の開発を目的とするのであれば、計算効率を優先させるべきではない。これは、「早すぎる最適化はプログラミングにおける諸悪の根源 (あるいは少なくともそのほとんど)」という言葉に集約される (Knuth 1974)。

アルゴリズム開発は大変な作業である。このことは、Base R を使った重心アルゴリズムの開発に費やした作業量から明らかである。このアルゴリズムは、実世界での応用が限られている問題に対する一つの、むしろ非効率的なアプローチに過ぎない。というのも、実際には凸ポリゴンは珍しいからである。この経験は、GEOS や CGAL (計算幾何学アルゴリズムライブラリ, Computational Geometry Algorithms Library) など、高速に動作し、かつ幅広い入力ジオメトリタイプに対応する低レベル地理ライブラリの理解につながるはずである。このようなライブラリのオープンソース化の大きな利点は、そのソースコードが、研究、理解、(技術と自信があれば) 改変のために容易に利用できることである。⁸¹

11.4 関数

アルゴリズムと同様に、関数は入力を受け取り、出力を返す。しかし、関数は、「レシピ」そのものではなく、特定のプログラミング言語での実装を指している。 R では、関数はそれ自体がオブジェクトであり、モジュール方式で作成したり結合したりすることができる。例えば、重心生成アルゴリズムのステップ 2 を引き受ける関数を以下のように作成することができる。

t_centroid = function(x) {
  (x[1, ] + x[2, ] + x[3, ]) / 3
}

上記の例では、関数の 2 つの重要な構成要素を示している。(1) 関数の中身 (body) は、中括弧内のコードで、関数が入力に対して何をするかを定義する。 (2) 引数 (argument) は、関数が扱う引数のリスト。この場合は x である (3 番目の重要なコンポーネント、環境はこのセクションの範囲外)。デフォルトでは、関数は最後に計算したオブジェクトを返す (t_centroid() の場合は重心の座標)。⁸²

この関数は、前のセクションのポリゴンの例から最初の三角形の面積を計算する以下のコマンドのように、渡した入力に対して動作する (Figure 11.3 を参照)。

t_centroid(T1)
#> x_coords y_coords 
#>     14.0     11.7

また、三角形の面積を計算する関数を作成することができる。ここでは、t_area() と名付ける。

t_area = function(x) {
  abs(
    x[1, 1] * (x[2, 2] - x[3, 2]) +
    x[2, 1] * (x[3, 2] - x[1, 2]) +
    x[3, 1] * (x[1, 2] - x[2, 2])
  ) / 2
}

なお、この関数を作成した後は、1 行のコードで三角形の面積を計算できるようになり、冗長なコードの重複を避けることができる。関数は、コードを一般化するためのメカニズムである。新たに作成した関数 t_area() は、これまで使ってきた「三角行列」データ構造と同じ寸法を持つと仮定した任意のオブジェクト x を受け取り、その面積を返すもので、T1 で図示すると次のようになる。

t_area(T1)
#> [1] 85

関数を使って、高さ 1、底辺 3 の新しい三角行列の面積を求めることで、その一般化可能性を検証することができる。

t_new = cbind(x = c(0, 3, 3, 0),
              y = c(0, 0, 1, 0))
t_area(t_new)
#>   x 
#> 1.5

関数の便利な点は、モジュール化されていることである。出力が何であるかが分かっていれば、ある関数を別の関数の構成要素として利用することができる。したがって、関数 t_centroid() と t_area() は、スクリプト 11-centroid-alg.R というより大きな関数のサブコンポーネントとして使うことができる。このスクリプトは、任意の凸ポリゴンの面積を計算する。以下のコードでは、凸ポリゴンに対する sf::st_centroid() の動作を模倣する関数 poly_centroid() を作成している。⁸³

poly_centroid = function(poly_mat) {
  Origin = poly_mat[1, ] # create a point representing the origin
  i = 2:(nrow(poly_mat) - 2)
  T_all = lapply(i, function(x) {rbind(Origin, poly_mat[x:(x + 1), ], Origin)})
  C_list = lapply(T_all, t_centroid)
  C = do.call(rbind, C_list)
  A = vapply(T_all, t_area, FUN.VALUE = double(1))
  c(weighted.mean(C[, 1], A), weighted.mean(C[, 2], A))
}

poly_centroid(poly_mat)
#> [1] 8.83 9.22

poly_centroid() などの関数はさらに拡張して、さまざまなタイプの出力を提供することができる。例えば、結果をクラス sfg のオブジェクトとして返すには、結果を返す前に、「ラッパー」関数を用いて poly_centroid() の出力を変更することができる。

poly_centroid_sfg = function(x) {
  centroid_coords = poly_centroid(x)
  sf::st_point(centroid_coords)
}

以下のように、sf::st_centroid() からの出力と同じであることが確認できる。

poly_sfc = sf::st_polygon(list(poly_mat))
identical(poly_centroid_sfg(poly_mat), sf::st_centroid(poly_sfc))
#> [1] TRUE

11.5 プログラミング

この章では、スクリプトからアルゴリズムという厄介なトピックを経由して関数へと移った。抽象的な議論だけでなく、具体的な問題を解決するために、それぞれの実用例を作成した。

スクリプト 11-centroid-alg.R を導入し、「ポリゴンマトリックス」で実行した。
このスクリプトを動作させるための個々のステップは、アルゴリズム、つまり計算レシピとして記述した。
アルゴリズムを一般化するために、このアルゴリズムをモジュール関数に変換し、最終的にそれらを組み合わせて、前節の関数 poly_centroid() を作成した。

これらのステップは、簡単なことである。しかし、プログラミングの技術とは、スクリプト、アルゴリズム、関数を組み合わせて、性能の良いシステムにすることなのである。できたものは、堅牢で、皆が簡単に使えるものであるべきである。この本を読んでいるほとんどの人がそうであるように、プログラミングの初心者であれば、前のセクションの結果を追って再現できることは、大きな達成感を得ることができるはずである。プログラミングができるようになるまでには、何時間もかけて熱心に勉強し、練習する必要がある。

新しいアルゴリズムを効率的に実装する際の課題は、実運用で使用することを意図していない単純な関数を作成するために費やした作業量を考慮すると、はるかに遠い。現在の状態では、poly_centroid() はほとんどの (非凸) ポリゴンで失敗する! ここから生じる疑問は、関数をどのように一般化するかということである。 (1) 非凸ポリゴンを三角測量する方法を探す (geocompx.github.io/geocompkg/articles/ のオンライン記事 Algorithms Extended で扱っている話題) と (2) 三角メッシュに依存しない他の重心のアルゴリズムを調べるという 2 つの選択肢がある。

もっと大きな疑問は、高性能なアルゴリズムがすでに実装され、st_centroid() のような関数にパッケージされているのに、ソリューションをプログラミングする価値があるのだろうか、ということである。この具体的なケースにおける還元論的な答えは「価値はない」である。広い意味で、プログラミングを学ぶことの利点を考えると、答えは「場合による」である。プログラミングでは、あるメソッドを実装しようとすると、すでに誰かがその苦労をしていることに気づき、何時間も無駄にすることがよくある。本章は、ジオアルゴリズムのプログラミングへの第一歩として捉えることができる。しかし、一般化された解決策をプログラムする場合と、既存の高水準の解決策を利用する場合の教訓とも言える。新しい関数を作るのが最善の場合もあれば、すでにある関数を使うのが良い場合もある。

「車輪の再発明をするな」という言葉は、他の人生の歩みと同様、いやそれ以上にプログラミングに当てはまる。プロジェクトの最初に少し調査して考えることで、プログラミングの時間をどこに費やすのがベストなのかを決めることができる。また、以下の 3 つの原則は、簡単なスクリプトであれ、何百もの関数で構成されるパッケージであれ、コードを書くときに労力を最大限に活用するのに役立つ。

DRY (don’t repeat yourself): コードの繰り返しを最小限に抑え、より少ないコード行数で特定の問題を解決することを目指す。この原則は、「R for Data Science」の「Functions」の章において、コードの繰り返しを減らすための関数の使用を参照して説明されている (Grolemund and Wickham 2016)。
KISS (keep it simple stupid): この原則は、複雑な解決策よりも単純な解決策を最初に試し、必要に応じて依存関係を使用し、スクリプトを簡潔に保つことを目指すことを示唆。この原則は、「ものごとはできるかぎりシンプルにすべきだ。しかし、シンプルすぎてもいけない。」“things should be made as simple as possible, but no simpler” という名言のコンピュータ版である。
Modularity: コードを明確に分割することで、メンテナンスが容易になる。関数は、たった一つのことをするだけにして、それに専念するべきである。もし関数が長くなりすぎたら、それを複数の小さな関数に分割し、それぞれを別の目的に再利用することを考えよう。

この章だけで、すぐに完璧な関数を作成できるようになることは保証していない。しかし、この章の内容は、いつ挑戦するのが適切かを判断するのに役立つと確信している (問題を解決する既存の関数がない場合、プログラミングタスクが自分の能力の範囲内にある場合、そのソリューションの利点が開発にかかる時間コストを上回ると思われる場合)。上記の原則と、上記の例を通しての実践的な経験を組み合わせることで、スクリプト、パッケージ作成、プログラミングのスキルを手に入れることができる。プログラミングへの最初の一歩は時間がかかるが (以下の演習は急がないように)、長期的な見返りは大きくなるだろう。

11.6 演習

E1. 本書の GitHub リポジトリの 11-centroid-alg.R スクリプトを読みなさい。

ベストプラクティスのうちどれを使っているか？
RStudio などの IDE を使い、自分のパソコンでスクリプトを作成しなさい (スクリプトを 1 行ずつ打ち込み、適宜コメントを入れると良い。コピペはしない。この作業でスクリプトの入力の仕方を学ぶことができる。)。正方形ポリゴン (poly_mat = cbind(x = c(0, 9, 9, 0, 0), y = c(0, 0, 9, 9, 0)) で作成) の例を使い、スクリプトを 1 行ずつ実行しなさい。
再現可能性を高めるためにはどのように変更したら良いか?
ドキュメンテーションをより良くするためにはどうしたら良いか?

E2. 幾何アルゴリズムのセクションで、poly_mat のポリゴンの面積は 245 で、重心は座標 (8.8, 9.2) であると計算した。

このアルゴリズムのスクリプトである 11-centroid-alg.R を参照し、自分のパソコンで結果を再現しなさい (ボーナス: コピペせずに自分で入力しなさい)。
結果は正しいか? poly_mat を st_polygon() 関数で sfc オブジェクトに変換し (poly_sfc という名前)、st_area() 関数と st_centroid() 関数を用いて検証しなさい (ヒント: この関数は、クラス list() を引数に取る)。

E3. 我々が作成したアルゴリズムは凸包に対してのみ動作すると記載されている。凸包を定義し (ジオメトリ操作の章を参照)、凸包でないポリゴンでアルゴリズムをテストしなさい。

ボーナス 1: なぜこの方法が凸の外皮に対してのみ機能するのかを考え、他の種類の多角形に対して機能させるためにアルゴリズムに加える必要がある変更点に注意する。
ボーナス 2: 11-centroid-alg.R の内容を基に、行列形式で表現された線分の全長を求めることができる、Base R 関数のみを使ったアルゴリズムを書きなさい。

E4. 関数のセクションでは、sfg クラスの出力 (poly_centroid_sfg()) と matrix 型の出力 (poly_centroid_type_stable()) を生成する poly_centroid() 関数の異なるバージョンを作成した。さらに、型が安定で (sf クラスの入力しか受け付けない) sf オブジェクトを返すバージョン (例えば poly_centroid_sf()) を作成し、関数を拡張しなさい (ヒント: sf::st_coordinates(x) コマンドでオブジェクト x を行列に変換する必要があるかもしれない)。

poly_centroid_sf(sf::st_sf(sf::st_sfc(poly_sfc))) を実行し、動作するか検証しなさい
poly_centroid_sf(poly_mat) を実行しようとした時、どのようなエラーメッセージが表示されたか?

10 GIS ソフトウェアへのブリッジ

12 統計的学習